Primzahlen bilden eine Grundlage der Mathematik und sind deshalb auch auf der Sekundarstufe I ein Thema. Allerdings beschränkt sich die Auseinandersetzung auf dieser Stufe häufig darauf, die Primzahlen mithilfe des Siebes von Eratosthenes zu gewinnen und diese anschliessend für die Primfaktorzerlegung von natürlichen Zahlen zu verwenden. Dabei bietet sich das Thema auf gut dafür an, die Berechnung von Primzahlen mit dem Computer und zu thematisieren und dabei über die Optimierung von Algorithmen zu diskutieren.
Naiver Ansatz
In einem ersten Versuch verwenden wir einen ganz einfachen Algorithmus. Wir nehmen zuerst einmal an, jede Zahl sei eine Primzahl. Dann teilen wir diese Zahl durch alle Zahlen, die kleiner als die gewünschte Zahl selbst sind. Sollten bei diesen Divisionen der Rest irgendwann 0 sein, verwerfen wir die Annahme, dass es sich um eine Primzahl handelt.
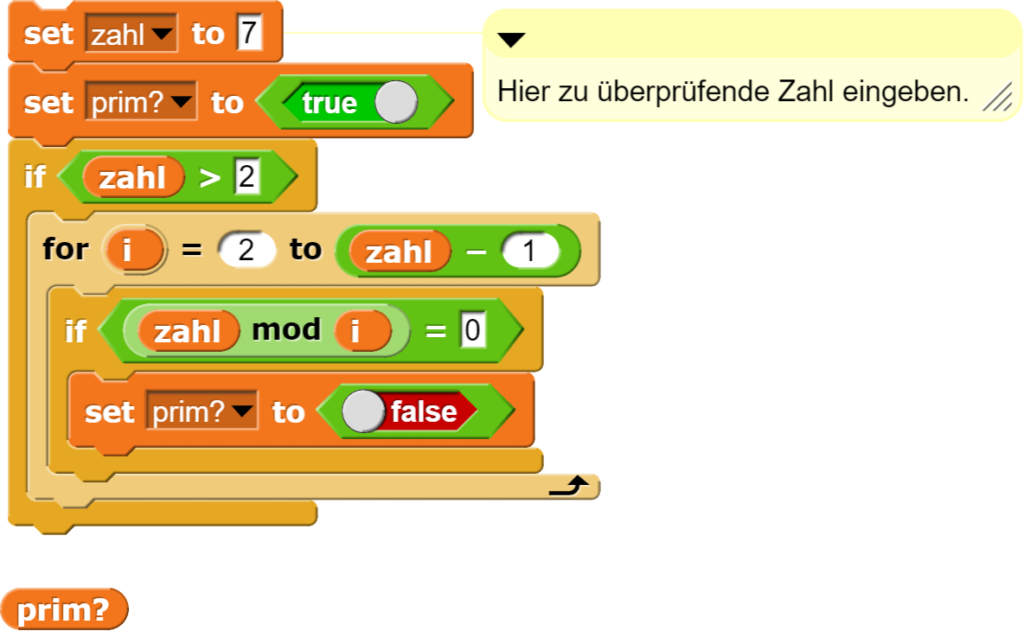
Dieser einfache Algorithmus funktioniert für Zahlen > 1 gut, ist aber sehr langsam, da viele unnötigen Berechnungen durchgeführt werden. Dies sieht man, wenn man alle Zahlen aufführt, welche bei den Divisionen verwendet werden.

Es fällt sofort auf, dass viele unnötige Rechenschritte durchgeführt werden, weil beispielsweise alle geraden Zahlen (ausser der 2) sicherlich keine Primzahlen sind. Trotzdem wird beispielsweise bei der 50 noch lange weitergerechnet, selbst wenn schon früh klar ist, dass es sich nicht um eine Primzahl handeln kann.
Möglichst frühzeitiger Abbruch
Die Vermeidung unnötiger Rechenschritte bedingt die Neuformulierung des Algorithmus. Dafür muss die for-Schleife in Snap! durch eine while-Schleife ersetzt werden. Allerdings steht diese nicht standardmässig zu Verfügung, weshalb diese zuerst programmiert werden muss. In Snap! funktioniert dies wie folgt:
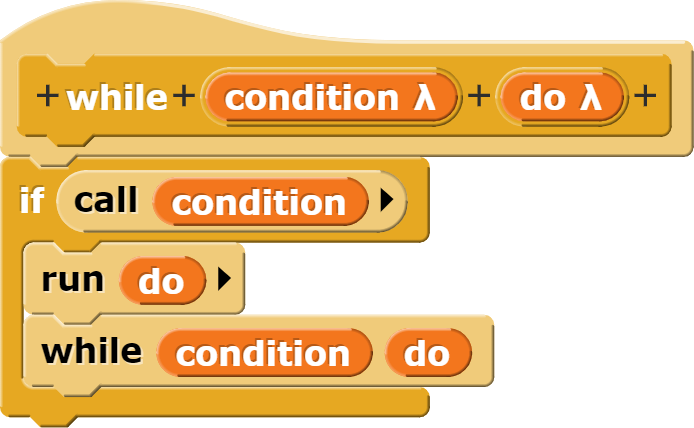
Mit der durch die while-Schleife mögliche Anpassung des Algorithmus werden unnötige Rechenschritte verhindert.
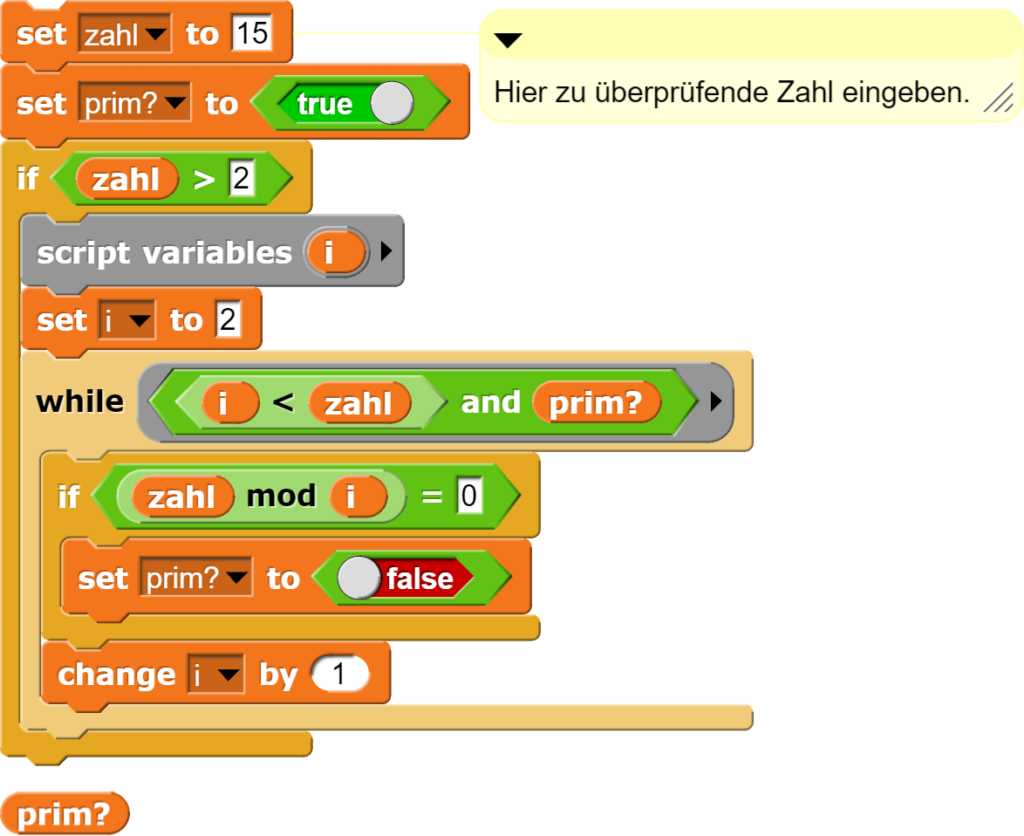
Dies wird deutlich, wenn man sich noch einmal alle Zahlen anschaut, die nun in den notwendigen Divisionen verwendet werden.
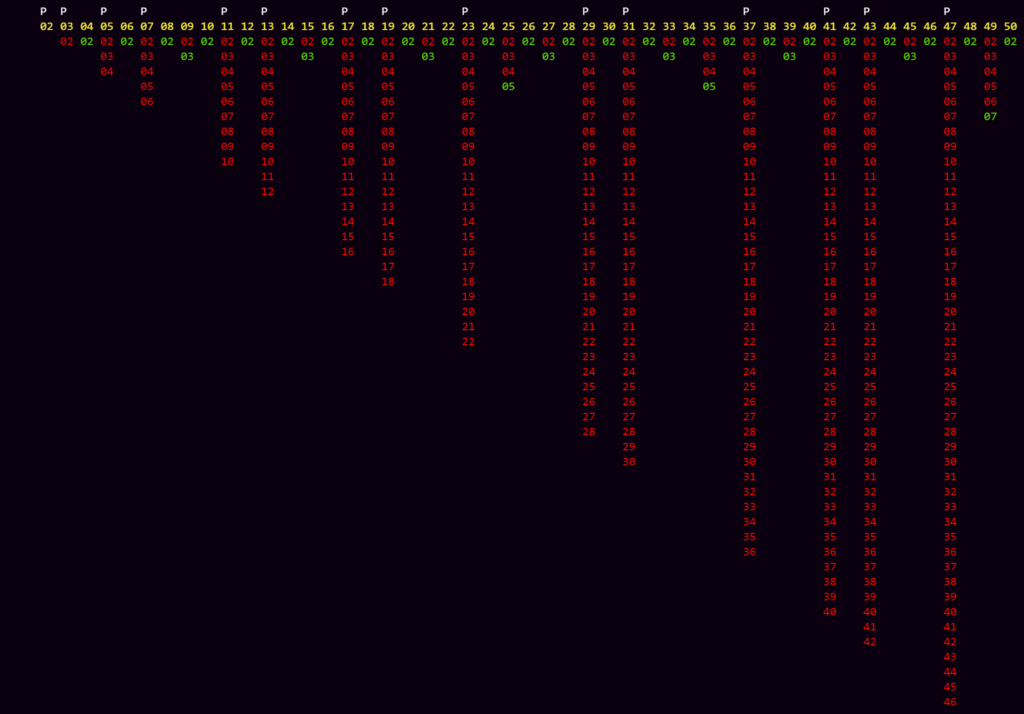
Bei allen Zahlen, welche keine Primzahlen sind, wird die Berechnung schon sehr früh abgebrochen. Dies ist auch deshalb von Interesse, weil Primzahlen seltener werden, wenn man grössere Zahlen untersucht. Das wird bereits in der oben abgebildeten Grafik deutlich:
- Zahlenraum 1-25: 2, 3, 5, 7, 11, 13, 17, 19, 23, insgesamt 9 Primzahlen.
- Zahlenraum 26-50: 29, 31, 37, 41, 43, 47 , insgesamt 6 Primzahlen.
Um das Programm weiter zu optimieren, ist eine mathematische Betrachtung von Teilern notwendig.
Eigenschaften von Teilern
Die Teiler einer bestimmten Zahl treten immer paarweise auf, wobei es vorkommen kann, dass die beiden Teiler gleich gross sind:
- Teiler von 12: 1 und 12, 2 und 6, 3 und 4.
- Teiler von 25: 1 und 25, 5 und 5.
Zu jedem grossen Teiler gehört also ein entsprechend kleiner Teiler. Bei der Quadratzahl 25 ist gut ersichtlich, dass zum Teiler 5 kein Teiler vorhanden ist, der grösser als 5 ist, sonst müsste es sich, z.B. bei 5 x 6 um eine grössere Zahl handeln.
Damit ist es möglich, die zu überprüfenden Teiler weiter einzuschränken. Statt bei Primzahlen bis zu n-1 zu prüfen, reicht eine Prüfung bis zur Quadratwurzel von n aus.
Die Änderung im Algorithmus beschränkt sich dabei auf das Abbruchkriterium in der while-Schleife.

Dadurch verringert sich der Rechenaufwand bei den bisher aufwändigen Primzahlen noch einmal dramatisch, was die Auflistung der benötigten Teiler zeigt:

Eine weitere Optimierung ist möglich, indem man nicht mehr alle Zahlen als Teiler verwendet, sondern nur noch die Primzahlen selbst. Dabei stellt sich aber die Frage, woher dann diese Primzahlen im Voraus bekannt sein sollen.
Nimm 2
Mit einem entsprechenden höheren Aufwand beim Schreiben des Algorithmus ist es tatsächlich möglich, die Primzahlen aus sich selbst heraus zu erzeugen. Als Voraussetzung wird dazu nur eine Liste mit dem Element 2 benötigt. Alle weitere Primzahlen kann das folgende Programm daraus generieren.
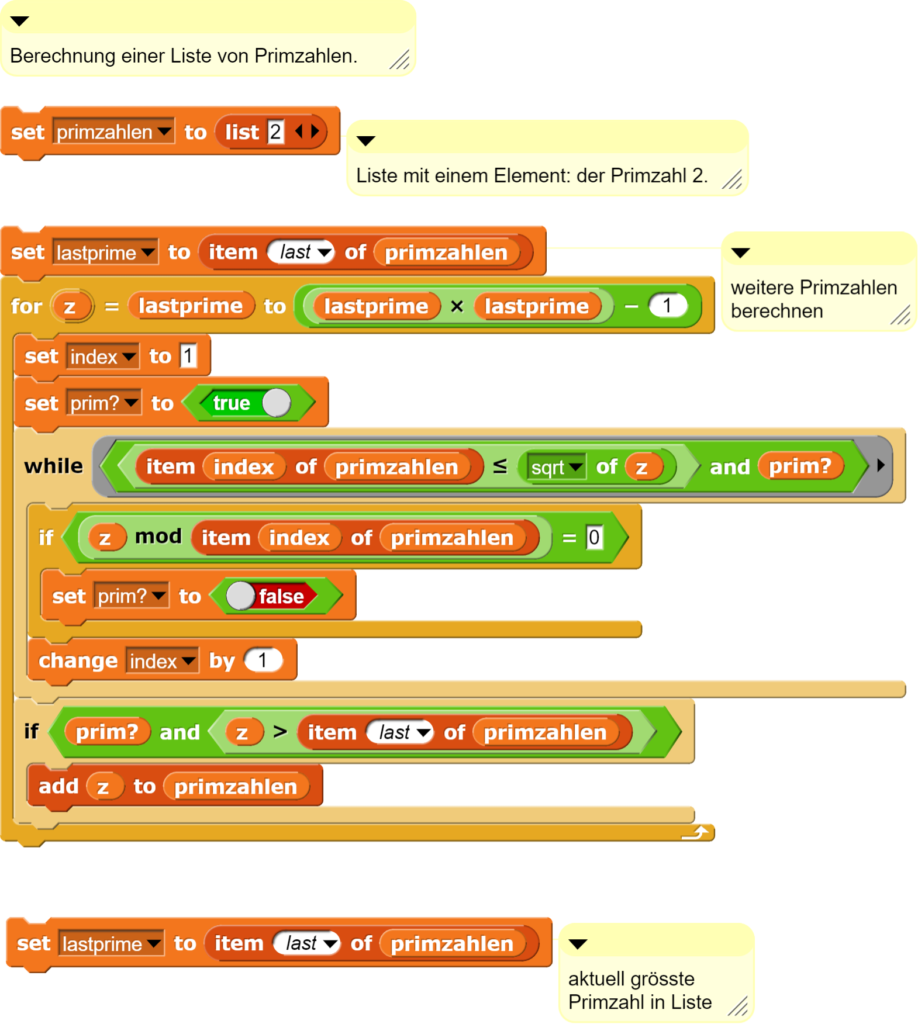
Nach dem ersten Durchlauf des Programms besteht die Liste aus den Zahlen 2 und 3, denn es wird bis maximal zur Zahl 3 geprüft und diese ist nicht durch 2 teilbar. Nach dem zweiten Durchlauf sind die Primzahlen 5 und 7 dazugekommen, denn das Programm prüft nun bis 8. Der nächste Durchlauf prüft bis 48 und liefert als letzte Primzahl 47 zurück. Bei jedem weiteren Durchlauf wird der untersuchte Zahlenraum grösser und damit die Liste der Primzahlen länger. So können aus der 2 alle weiteren Primzahlen generiert werden.
Nebst der schnelleren Berechnung hat dieser Ansatz auch den Vorteil, dass die Berechnung der Primzahlen jederzeit angehalten und später wieder fortgesetzt werden kann. Denn alles, was das Programm dafür benötigt, ist die Liste mit den Primzahlen, aus welcher es die grösste Primzahl ausliest, um weitere Berechnungen anzustellen.
Im gezeigten Beispiel darf der Computer dazu nicht ausgeschaltet werden, da sich die Liste im flüchtigen Speicher befindet. Die geführte Liste könnte aber auch auf eine Harddisk geschrieben werden, wodurch das Programm seine Arbeit auch nach einem tatsächlichen Unterbruch wieder aufnehmen könnte.
Laufzeiten
Die Laufzeiten der unterschiedlichen Varianten unterscheiden sich dramatisch. Gemessen wurde jeweils die Zeit, welche zur Berechnung der ersten n Primzahlen notwendig war.
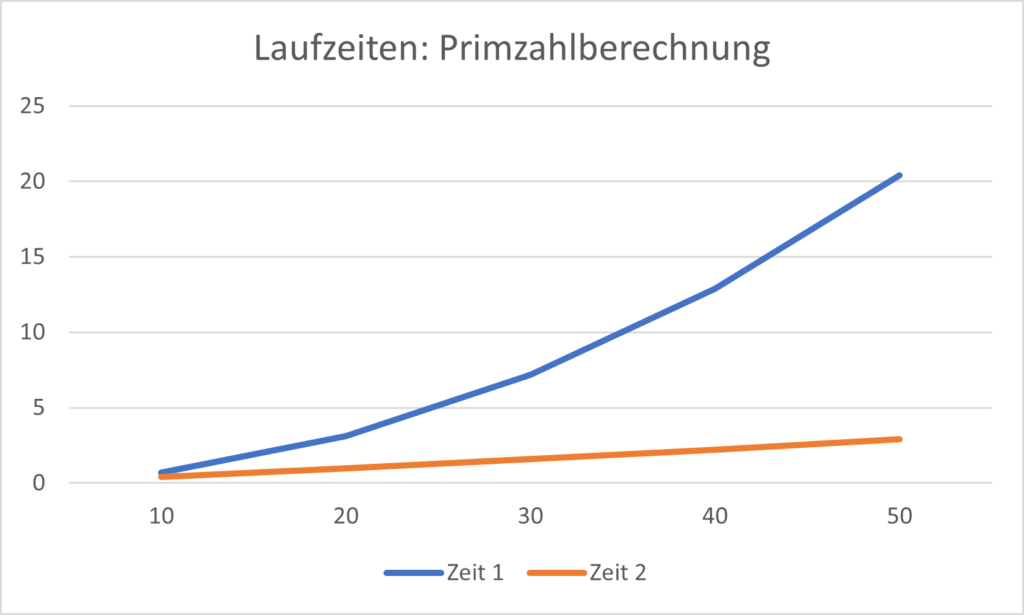
Während bei der einfachsten Version die Laufzeiten immer stärker zunehmen, verhalten sich diese in der optimierten Fassung zumindest im untersuchten Zahlenbereich fast linear. Diese Unterschiede sind bei kleinen Zahlenbereich noch klein, werden aber schnell immer grösser.
Anwendung im Unterricht
Die vorgestellten Ansätze können nicht nur dafür verwendet werden, bei grösseren Zahlen herauszufinden, ob es sich dabei um Primzahlen handelt. Sie bieten auch eine gute Gelegenheit dafür, mit den Schülerinnen und Schülern die Notwendigkeit der Optimierung von Programmen zu besprechen.
Diese spielt bei vielen Computeranwendungen eine wichtige Rolle, nicht nur weil dadurch Energie und die damit verbundenen Kosten eingespart werden können, sondern dadurch werden auch Anwendungen möglich, die vorher aus Zeitgründen nicht praktikabel umgesetzt werden konnten.
