Wahrscheinlichkeit für einen kürzbaren Bruch

Im Lehrmittel „Mathematik I“ für die Sekundarstufe wird im Arbeitsheft 1 auf Seite 141 folgende Tüftelaufgabe gestellt: Wie wahrscheinlich ist es, dass ein Bruch gekürzt werden kann, wenn dessen Zähler und Nenner jeweils aus einer zufälligen Zahl von 2 bis 9 gebildet werden?

Eine solche Aufgabe bietet sich förmlich dazu an, mit einem Computerprogramm gelöst zu werden. Ausserdem wird es dadurch möglich, die Aufgabenstellung zu verallgemeinern.

Ursprüngliche Aufgabe mit Snap! lösen

Ein klassisches Vorgehen zum Lösen dieser Aufgabe könnte so aussehen:

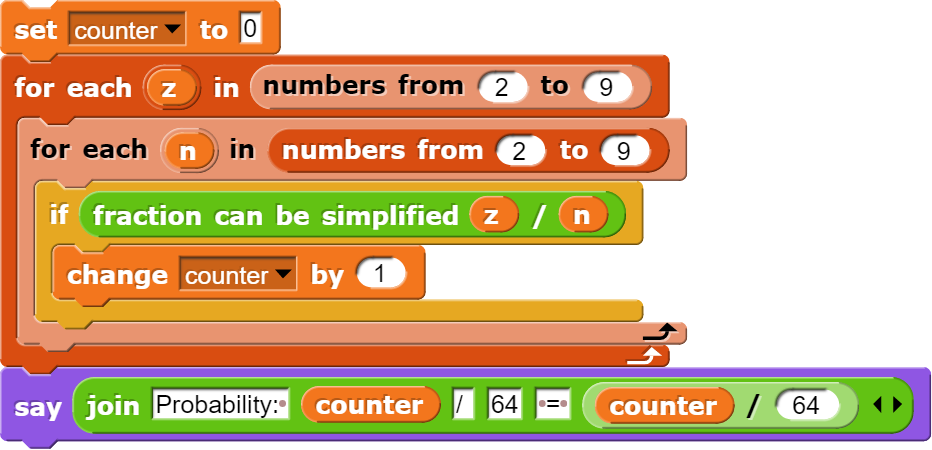
Mathematisch betrachtet kann ein Bruch dann gekürzt werden, wenn die Zähler und Nenner einen gemeinsamen Teiler besitzen, der grösser ist als 1. Der Block für die Berechnung des ggTs kann in Snap! aus der Bibliothek „APL Primitives“ importiert werden und heisst dort gcd (engl. greatest common denominator).

Damit kann nun der Block „fraction can be simplified“ entsprechend programmiert werden.

Lässt man das Programm laufen, berechnet es den korrekten Wert von 26/64 oder 40.625%. Allerdings ist die for-Schleife in Snap! nicht besonders effizient. Deshalb soll das gleiche Programm nun mit dem map-Block umgesetzt werden, was nebst einem Geschwindigkeitsgewinn weitere Vorteile mit sich bringt.

Zuerst sollen mit dem map-Block erst einmal nur die Brüche erzeugt werden:

Die Werte des äusseren map-Blockes werden dabei über den Parameter „value“ an den inneren map-Block weitergegeben. Der „value“-Parameter kann über einen Klick auf das kleine Dreieck im map-Block sichtbar gemacht werden.

Speichert man das Ergebnis der Berechnung in einer Variablen ab, kann man dieses sichtbar machen.

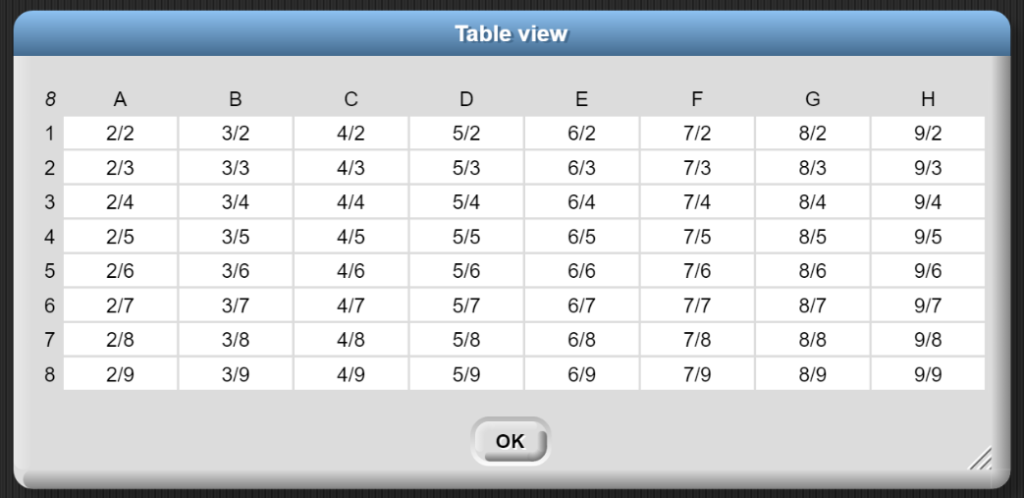
Nebst der schnelleren Durchführung der entsprechenden Rechenoperationen erhält man als Bonus noch eine Darstellung, welche im Gegensatz zur Variante mit der for-Schleife besser nachvollziehbar ist.

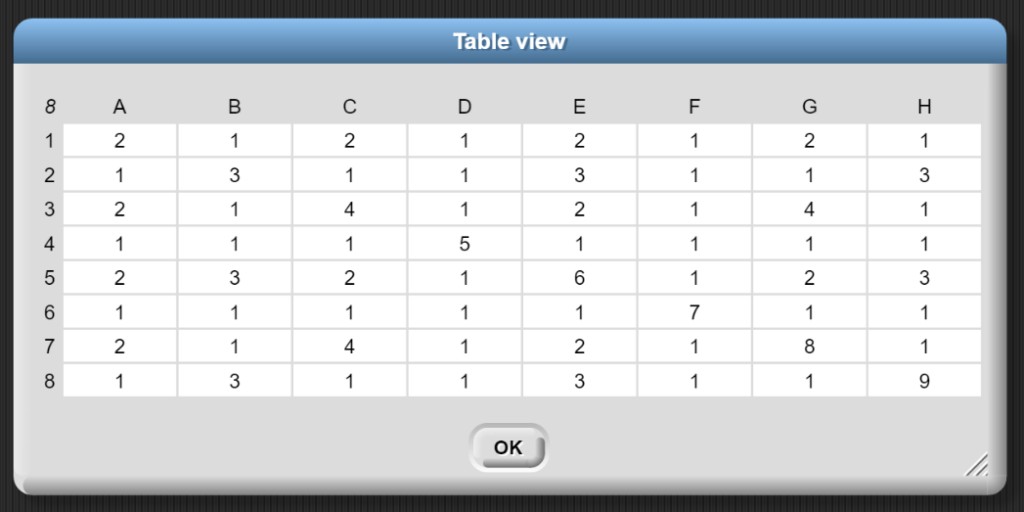
Wird nun der join-Block durch die Berechnung des ggTs ersetzt, erhält man auch die entsprechenden Werte in Tabellenform.

In der entsprechenden Tabelle werden nun die Werte sichtbar, mit denen die einzelnen Brüche gekürzt werden können.

Nun müssen nur noch die Fälle ausgezählt werden, bei denen der ggT grösser als 1 ist. Der schnellste Weg dazu ist die Verwendung des keep-Blockes, der die Tabelle auf die Zellen mit den gewünschten Werten reduziert. Damit dies funktioniert, muss die Tabelle allerdings zuerst noch in eine Liste umgewandelt werden, wozu aber auch ein entsprechender Befehl zu Verfügung steht.

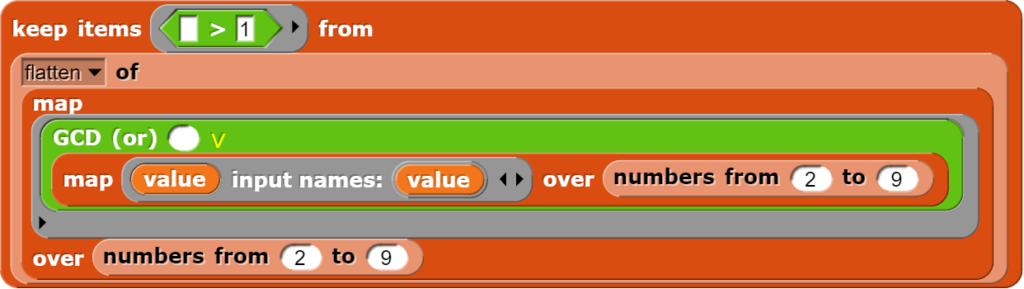
Um die Anzahl der Einträge in der so erhaltenen Liste zu bestimmen, verwendet man noch den length-Block und kann diesen Wert wie weiter oben gezeigt durch die Anzahl aller Fälle (64) dividieren.

Verallgemeinerung der Problemstellung

Die Verwendung des map-Blockes hat gegenüber der Variante mit der for-Schleife zu einer besser nachvollziehbaren Repräsentation geführt. In der Verallgemeinerung des Problems soll nun auch der Geschwindigkeitsvorteil ausgespielt werden, indem nicht mehr nur ein Fall, sondern mehrere untersucht werden sollen, indem die Frage beantwortet wird, wie wahrscheinlich es eigentlich ist, dass ein beliebiger Bruch gekürzt werden kann. Dazu wird der zuletzt abgebildete Block in einen Funktionsblock verpackt.

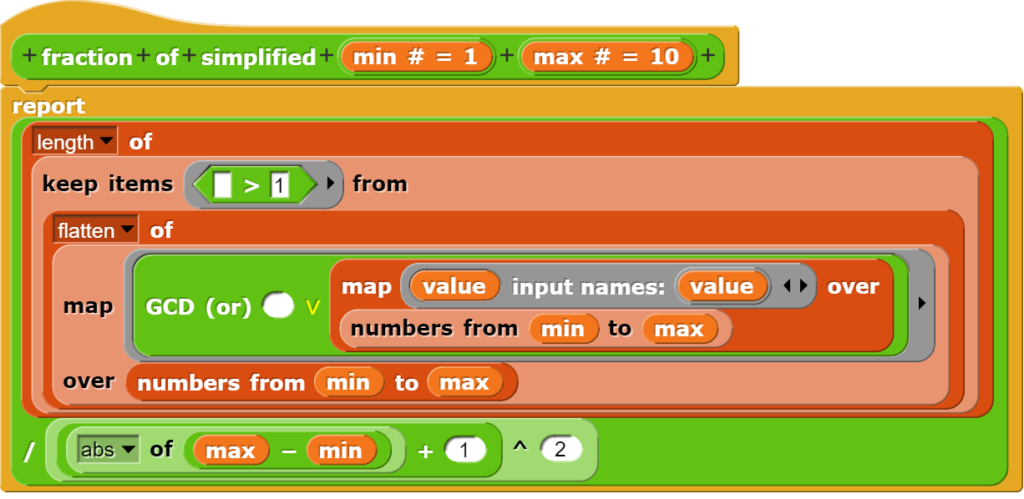
Diesen Block setzen wir nun so ein, dass Bruchtabellen mit den Dimensionen 1×1 bis 100×100 berechnet werden und für jede Tabelle die Wahrscheinlichkeit bestimmt wird, dass ein beliebiger Bruch in dieser Tabelle gekürzt werden kann.

Die Berechnung von 100 Werten nimmt etwas Zeit in Ansprung, ist aber viel schneller, als wenn das Problem mit der Technik der for-Schleifen gelöst wird.

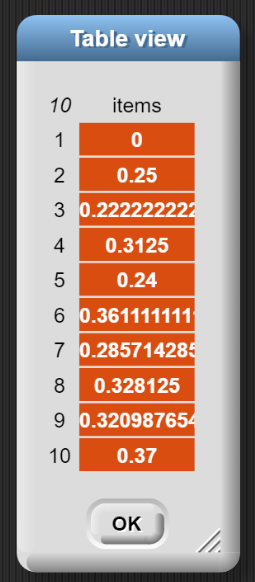
Da eine Liste mit 100 Werten recht unübersichtlich ist, sollen diese nun noch grafisch ausgegeben werden, dazu eignet sich der plot-Block aus der „Frequency Distribution Analysis“-Bibliothek, der Werte als Balken- oder Liniengrafik darstellen kann.

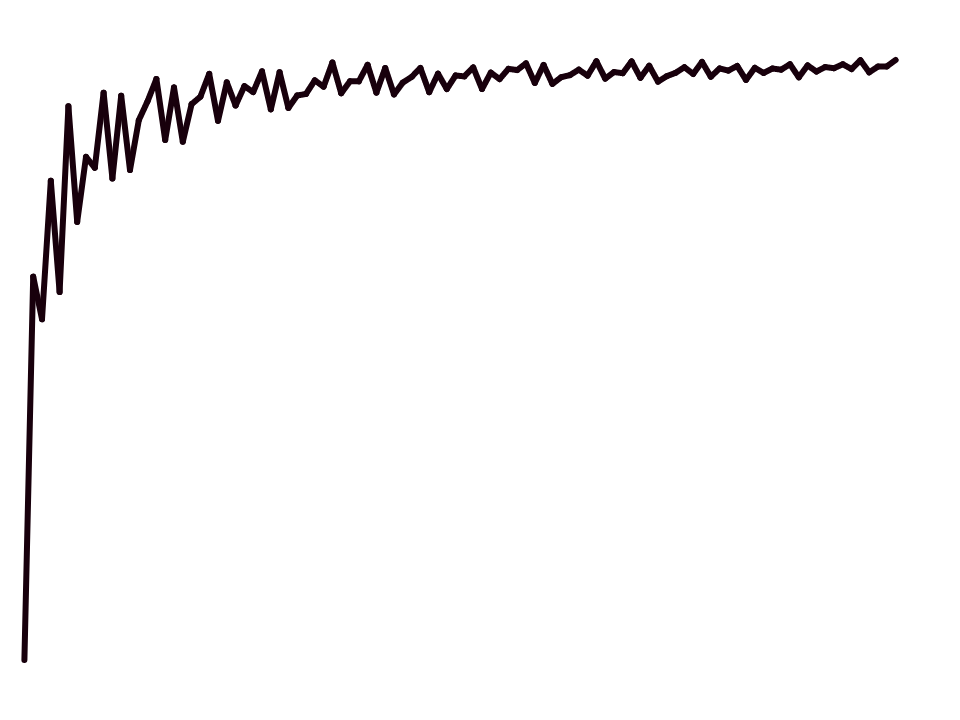
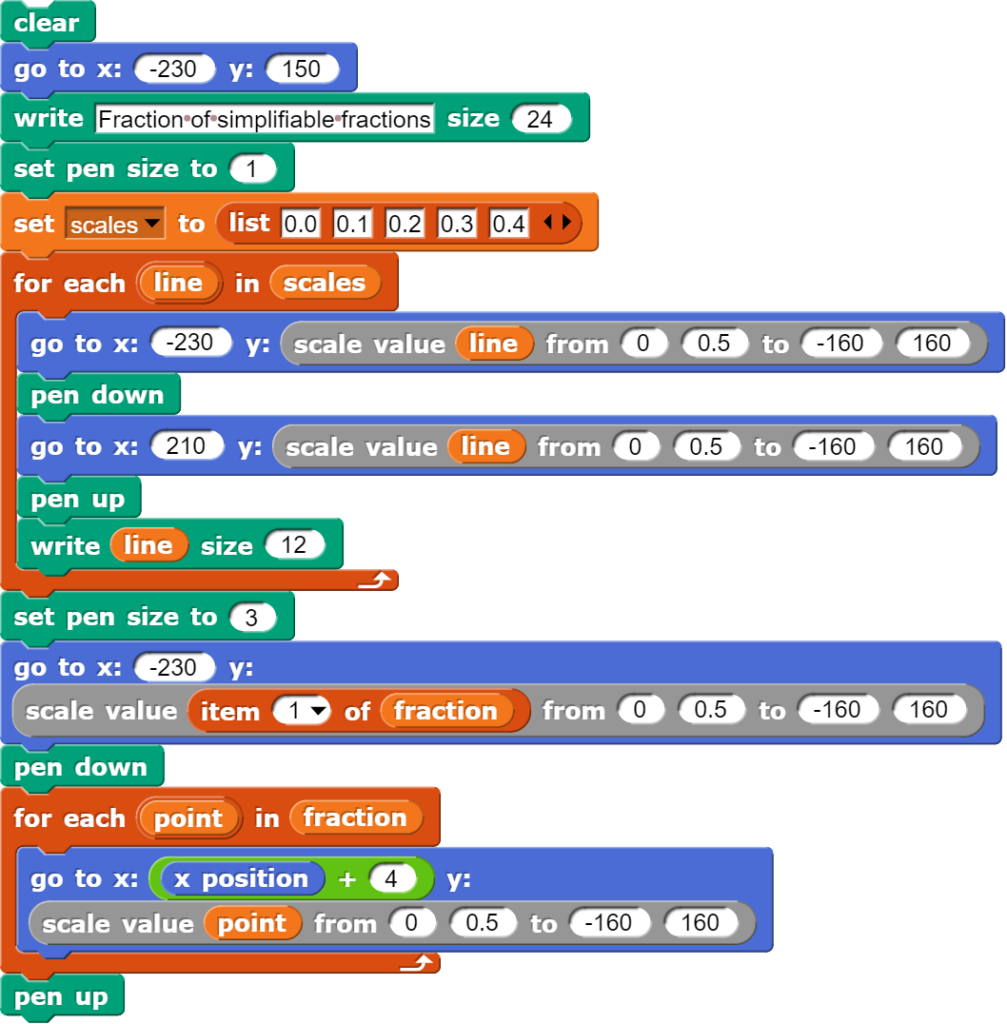
Falls die Grafik etwas professioneller gestaltet werden soll, dann muss etwas mehr Aufwand betrieben werden.

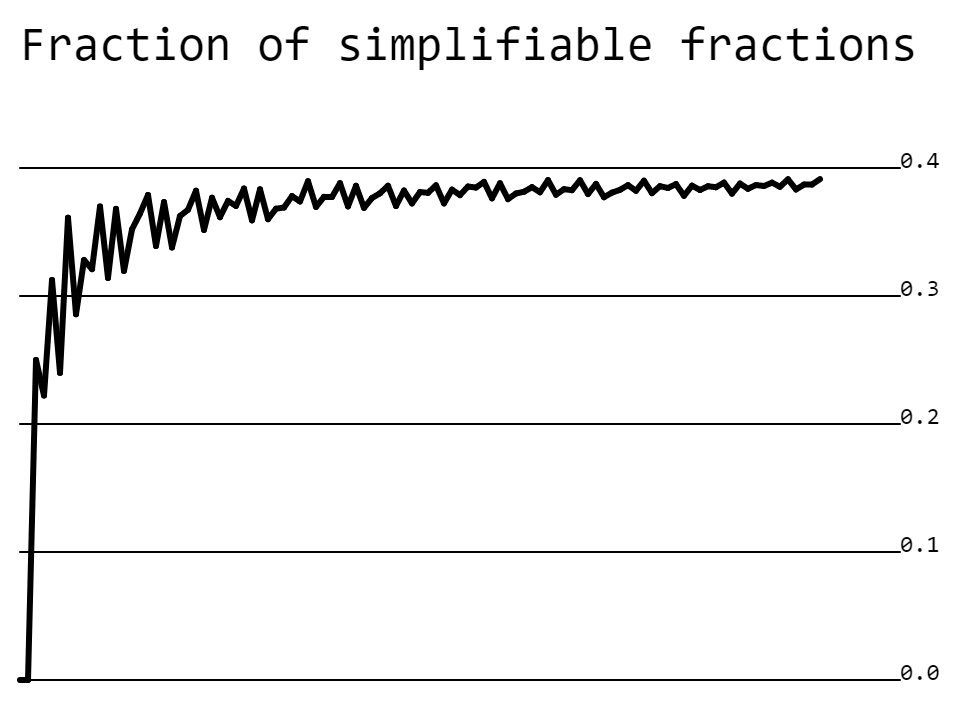
Wie schon in der einfachen Version der Grafik sind die Schwankungen der Wahrscheinlichkeiten in Abhängigkeit der einzelnen Bruchmengen deutlich erkennbar. Sie kommen dadurch zustande, dass neu hinzugekommene Werte nicht immer gleich viele Teiler haben. Kommt eine Primzahl neu dazu, sinkt die Wahrscheinlichkeit, besitzt die dazugekommene Zahl viele Teiler, steigt die Wahrscheinlichkeit. Es ist aber auch zu erkennen, dass die Werte bei grösseren Bruchmengen immer weniger schwanken. Eine Tatsache die auch bei anderen Zufallsexperimenten als „Gesetz der grossen Zahlen“ bezeichnet wird, wodurch sich der Kreis zum eigentlichen Thema der Wahrscheinlichkeit wieder schliesst.

Anwendung im Unterricht

Das vorgestellte Beispiel zeigt: Verzichtet man beim Lösen von Problemstellungen, wie sie hier vorgestellt wurde, auf die wiederholte Anwendung des Einsatzes von Bleistift und Papier und verwendet stattdessen den Computer, können Problemstellungen zwar nicht unbedingt schneller gelöst werden, denn die Entwicklung der entsprechenden Programmierung benötigt Zeit, aber die dadurch möglich werdende Flexibilisierung und Verallgemeinerung einer Aufgabenstellung erlaubt neue Ansichten und die Erweiterung einer geschlossenen Aufgabe zu einer weiter offenen, welche das Üben und die Anwendung wesentlicher Kompetenzen ermöglicht.