Zufallsexperimente mit Würfeln gehören zum Unterrichtsstoff der Sekundarstufe I. Im Zürcher Lehrmittel „Mathematik 1“ werden die Untersuchungen aber auf 2 Würfel beschränkt und auch der Lehrplan bleibt eher vage, wenn er von mehrstufigen Zufallsexperimenten mit Würfeln, Münzen und Zahlen spricht. An dieser Stelle soll deshalb gezeigt werden, wie die Thematik auch auf der Sekundarstufe I ausgebaut und damit ein erweiterter Blick in die Welt der Mathematik ermöglicht werden kann.
Würfeln mit einem Würfel
Den meisten Schülerinnen und Schülern ist klar, dass beim Würfeln mit 1 Würfel die Augensummen 1 bis 6 jeweils mit der gleichen Wahrscheinlichkeit auftreten.
Würfeln mit zwei Würfeln
Die Wahrscheinlichkeit des Auftretens einer gewissen Augensumme beim Würfeln kann ohne grossen Aufwand erarbeitet werden, indem man alle Möglichkeiten in einer zweidimensionalen Tabelle aufnotiert.
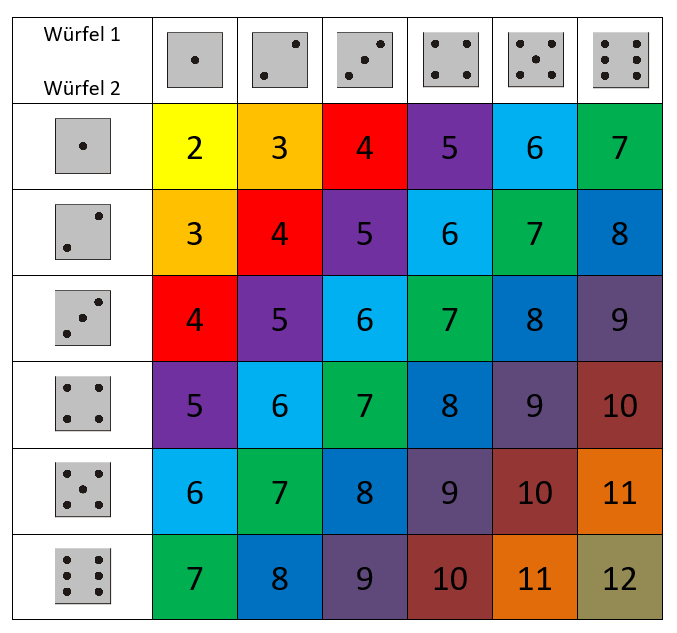
In diesem Zusammenhang kann nicht nur die Schreibweise für Wahrscheinlichkeiten eingeführt werden, sondern die Schülerinnen und Schüler können sich auch Gedanken darüber machen, welche Kombinationen von Augensummen für ein faires Spiel verwendet werden dürfen.
Würfeln mit drei Würfeln
Nach der linearen (1D) Darstellung der Augensummen bei einem Würfel und der Darstellung in der Fläche (2D) für zwei Würfel ist die Berechnung der Wahrscheinlichkeiten für die Augensummen beim Würfeln mit drei Würfeln erst einmal eine Herausforderung, weil die Darstellung in einem Würfel (3D) zwar naheliegt, deren Umsetzung aber zumindest auf Papier auf Schwierigkeiten stösst. Es lohnt sich deshalb, mit den Schülern darüber zu diskutieren, wie die einzelnen Ebenen des Würfels auf Papier auseinandergenommen werden können. Dies führt dann zu einer systematischen Notation in einer Tabelle, welche grundsätzlich für eine beliebige Anzahl von Würfeln funktioniert.
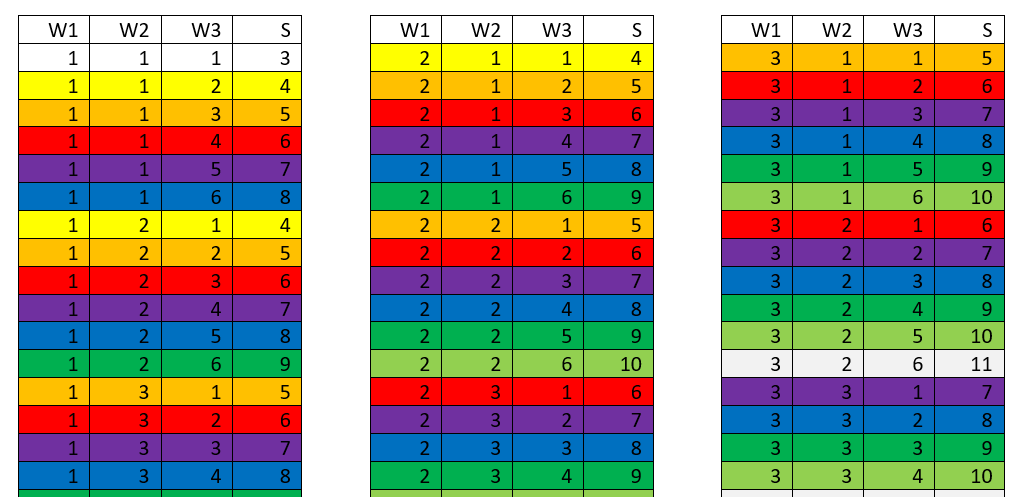
Alle 216 Möglichkeiten systematisch zu notieren, führt zum Ziel ist aber ziemlich aufwändig, weshalb sich beim Auszählen ein arbeitsteiliges Verfahren bewährt hat. Ausserdem ist für die meisten Schülerinnen und Schüler einsichtig, dass auch hier wieder eine Symmetrie der Wahrscheinlichkeiten der Augensummen auftritt. Einige Schülerinnen und Schüler versuchen den Arbeitsaufwand weiter zu reduzieren, indem sie theoretische Überlegungen über das Verhalten der verschiedenen Augensummen anstellen. In einem solchen Fall ist es hilfreich, wenn man sie darauf aufmerksam macht, dass insgesamt ja 216 unterschiedliche Fälle auftreten können, die sich dann in den verschiedenen Augensummen bündeln.
Würfeln mit vier Würfeln
Nach der Arbeit mit 3 Würfeln führt die Erwähnung einer Untersuchung für 4 Würfel meist zu wenig Begeisterung, denn die Schülerinnen und Schüler wissen zwar, dass die Aufgabe lösbar ist, aber gegenüber der eben geleisteten Arbeit einen sechsfach höheren Aufwand erfordert. Deshalb ist es an dieser Stelle sinnvoll, bei der Lösungssuche einen Strategiewechsel vorzunehmen und allenfalls vom Papier zum Computer in eine Tabellenkalkulation zu wechseln.
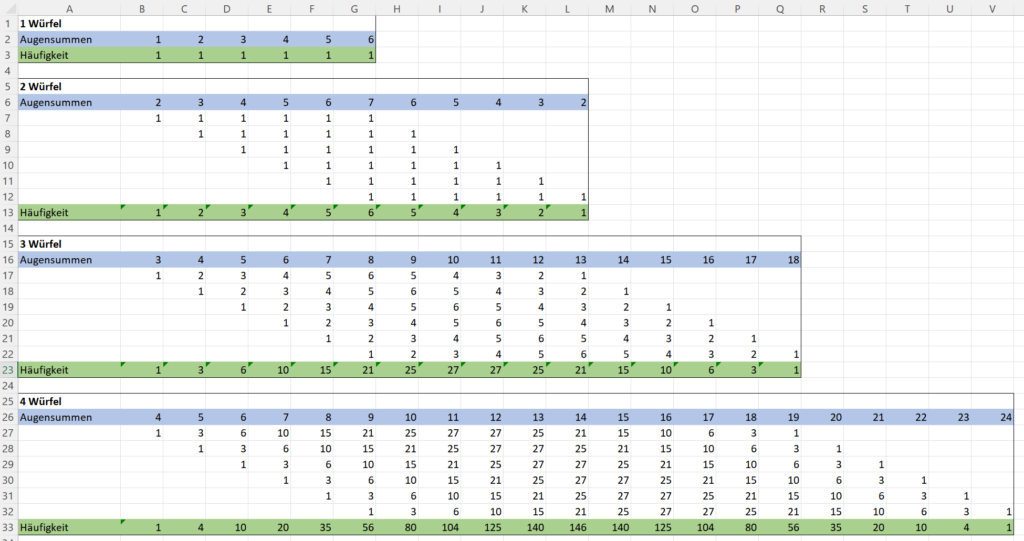
Um von dem Würfeln mit einem Würfel auf die Ergebnisse bei zwei Würfeln zu kommen, wurden in der Tabellenkalkulation einfach die schon vorhandenen Häufigkeiten verschoben notiert und anschliessend aufsummiert. Dadurch ergeben sich tatsächlich die Häufigkeiten für das Würfeln mit zwei Würfeln.
Ein genauerer Blick zeigt, wie die Resultate zustande kommen. Bei zwei Würfeln gibt es genau 1 Möglichkeit, die Augensumme 2 zu erzielen, nämlich dann, wenn der erste Würfel eine 1 zeigt und der zweite Würfel ebenfalls. Die Augensumme 3 hingegen kann auf 2 Arten erzielt werden: 1+2 und 2+1.
Genau die gleichen Überlegungen können beim Schritt von zwei zu drei Würfeln angestellt werden, wenn beispielsweise die Augensumme 5 gesucht wird, dann kann diese aus folgenden Kombinationen entstehen:
- (1, 1)+3, (1, 2)+2, (1, 3)+1 (drei Möglichkeiten),
- sowie (2, 1)+2 und (2, 2)+1 (2 Möglichkeiten)
- und schliesslich (3, 1)+1 (1 Möglichkeit).
Dieses Vorgehen kann analog für alle Augensummen durchgeführt werden und gilt für eine beliebige Anzahl von Würfeln. Die neuen Augensummen können immer durch das „verschobene“ Addieren der alten Häufigkeiten gewonnen werden.
Die Exceltabelle kann hier heruntergeladen werden: Tabelle_Augensummen.
Würfeln mit vielen Würfeln
Wie schon beim Schritt von drei auf vier Würfeln kann die beschriebene Methode für eine beliebige Anzahl von Würfeln verwendet werden. Allerdings steigt auch dabei der Arbeitsaufwand immer weiter an, wenn auch nicht so schnell wie beim Aufnotieren aller Fälle.
Deshalb ist es nun sinnvoll, einen Computer entsprechend zu programmieren. Traditionell würde dies mit einer mehrfach verschachtelten for-Schleife geschehen, deren genaue Funktionsweise aber nicht nur für Schülerinnen und Schüler schwer nachvollziehbar ist.
In Snap! gibt es mit den entsprechenden Listenfunktionen eine elegantere Lösung. In der Tabellenkalkulation wurden ja einfach „verschobene“ Häufigkeitswerte jeweils sechsmal addiert. Genau dies ist auch in Snap! möglich, wobei es keine Rolle spielt, wie lange die konkrete Liste ist.
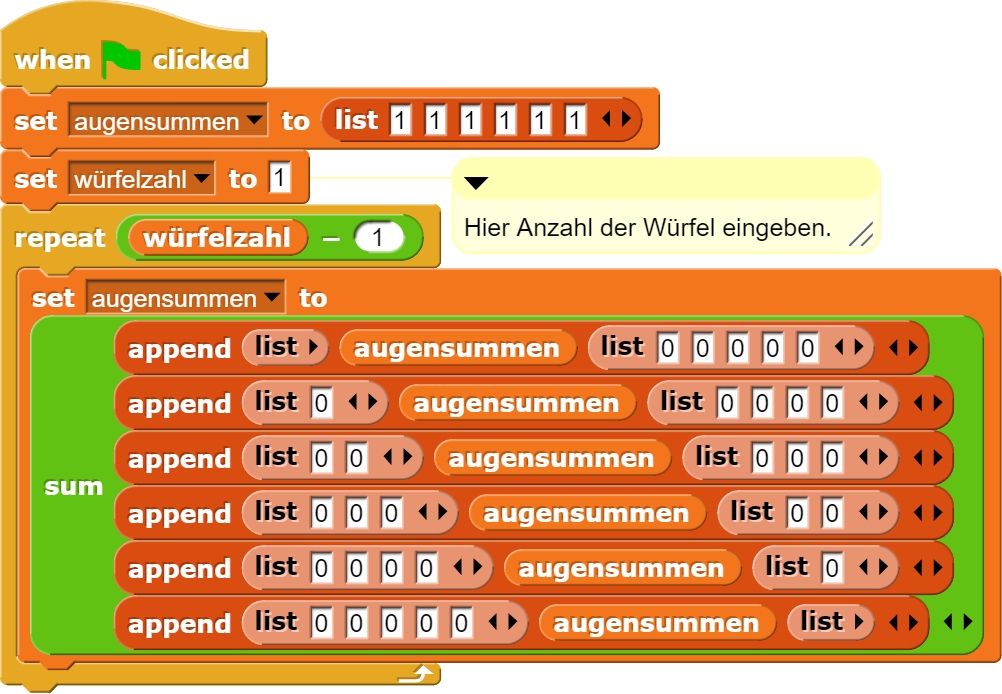
Zuerst wird die Liste „augensumme“ mit den Häufigkeitswerten für einen Würfel gesetzt. Dann wird die Anzahl der Würfel eingegeben und anschliessend berechnet das Programm durch wiederholtes Ausführen der „verschobenen“ Addition der bisherigen Werte die Häufigkeitswerte für den nächsten Würfel.
Wird der Block „set augensumme“ aus der Schleife herausgenommen, können die Schülerinnen und Schüler diesen wiederholt aufrufen und die dadurch neu entstehenden Listenwerte im Detail untersuchen. Augensummen beim Würfeln mit vielen Würfeln können anschliessend auch noch grafisch ausgegeben werden, was eine nächste Ebene der Betrachtung des Problems ermöglicht.
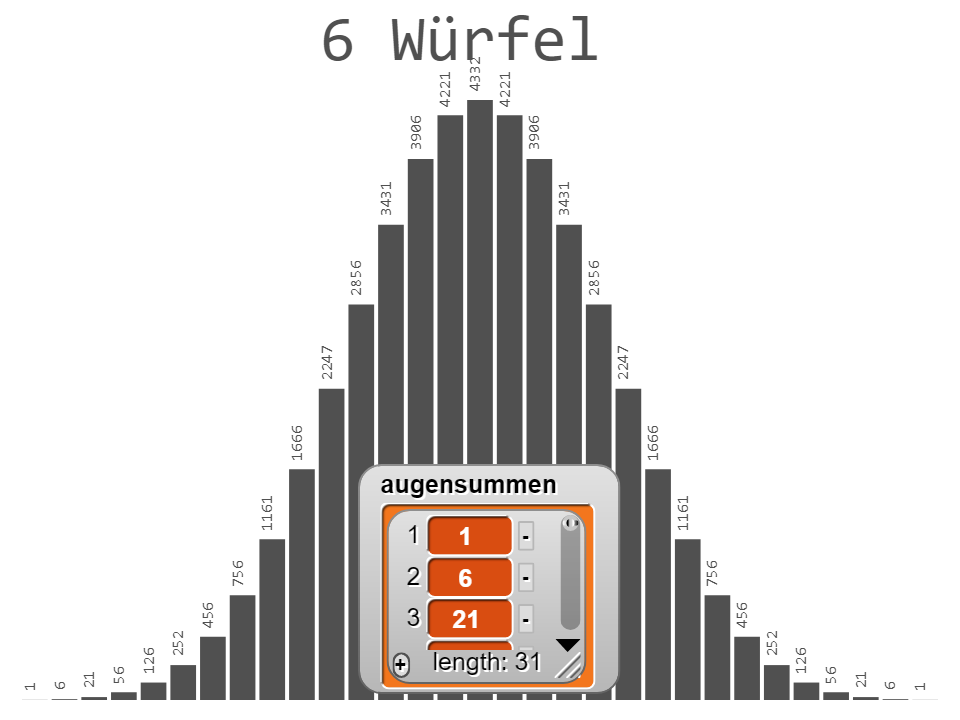
Das komplette Programm kann hier aufgerufen werden: Augensummen.
Weshalb der ganze Aufwand?
Dem Mathematikunterricht auf der Sekundarstufe I wird gerne vorgeworfen, er beschränke sich fast ausschliesslich auf die Vermittlung von Rechenverfahren, welche die Schülerinnen und Schüler dann möglicherweise beherrschten, aber nicht in einen grösseren Zusammenhang einordnen könnten.
Das vorgestellte Beispiel zeigt, dass es durchaus möglich ist, innerhalb eines vertretbaren Zeitrahmens (ca. 3 Lektionen) nicht nur den Bogen von einem sehr speziellen Problem zu einer allgemeineren Problemlösung zu schlagen, sondern durch unterschiedliche Repräsentationen auch gezielt mathematische Vorgehensweisen anzuwenden, die über das reine Hantieren mit Zahlen hinausgehen. Ausserdem wird dabei auch die Grundlage zur Erarbeitung weiterer mathematischer Konzepte gelegt. Dabei ist der Einsatz von Computern nicht zwingend notwendig, erleichtert aber durch die Automatisierung der zugrundeliegenden Rechenoperationen eine Konzentration auf die wesentlichen Aspekte der Problemstellung.
