Kategorie: Uncategorized

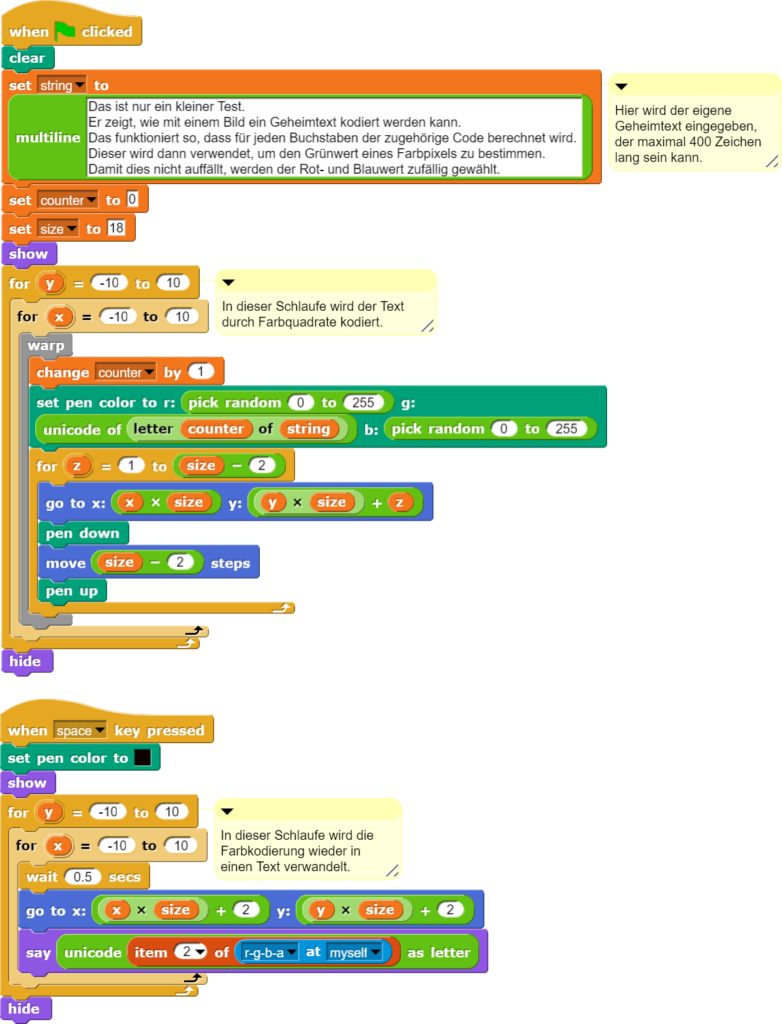
Online-Zeitungen, soziale Netzwerke und Plattformen wie YouTube erlauben es den Nutzerinnen und Nutzern, Inhalte zu veröffentlichen und diese zu kommentieren. Dabei halten sich nicht alle an die Grundregeln des Anstands: Sie verurteilen andere und versuchen diese zu demütigen oder zu entmenschlichen. Wie dieser Missbrauch der freien Meinungsäusserung im Unterricht thematisiert werden kann, zeigt eine Lektionsbeschreibung zu YouTube-Kommentare über Greta Thunberg.

Dazu schauten sich die Schülerinnen und Schüler ein auf YouTube veröffentlichtes Nachrichtenvideo der ARD Tagesschau an:

Im Anschluss füllten sie einen Fragebogen aus, bei dem sie zu verschiedenen Aussagen Stellung nehmen mussten.

Die Ergebnisse zeigen, dass die Schüler das Video für vertrauenswürdig halten, sie der Klimawandel beschäftigt und ihnen respektvolles Verhalten anderen gegenüber wichtig ist. Kritischer schätzen sie die Person von Greta Thunberg ein und die Bewegung „Fridays for Future“ ein, während sie davon ausgehen, dass der Klimawandel für Erwachsene nicht die gleich hohe Priorität hat wie für Jugendliche.

In der Umfrage konnten sich die Schülerinnen und Schüler auch frei über Greta Thunberg äussern. Einige Kommentare sollen dies verdeutlichen.

„Ich finde sie sieht sehr selbstbewusst aus. Sie sieht sympathisch aus und sie sieht jünger aus als sie ist. Ich glaube sie setzt sich sehr für das was sie macht ein und sie verbringt viel Zeit damit, darüber nachzudenken.“

„Greta sieht in meinen Augen recht jung aus, doch vom Verhalten würde ich sie älter schätzen. Mich persönlich interessiert es nicht, was sie macht.“

Im Anschluss hatten die Schülerinnen und Schüler Gelegenheit, die in einem PDF zusammengefassten Kommentare unter dem YouTube-Video zu studieren. Da das Dokument rund 200 Seiten umfasste, beschränkten sie sich jeweils auf Teilaspekte:

• Im einfachsten Falle lassen sie einfach einen Ausschnitt des Dokuments, d.h. beschränkten sich auf wenige Seiten.
• Andere benutzten die Suchfunktion des PDF-Betrachters um gezielt nach Begriffen zu suchen.
• Einige konzentrierten sich darauf, die Anzahl der Kommentare durch individuelle Nutzer zu zählen.

Den Schülerinnen und Schülern wurde schnell klar, dass das Video nicht nur wohlwollend kommentiert wurde, was sie teilweise stark irritierte.

Nach dem Studium der Kommentare beantworteten die Schülerinnen und Schüler eine zweite Umfrage. Dabei nahmen sie noch einmal zu den schon in der ersten Umfrage vorgegebenen Aussagen Stellung. Während die meisten Aussagen stabil bewertet wurden, kam es aber auch zu einigen interessanten Abweichungen:

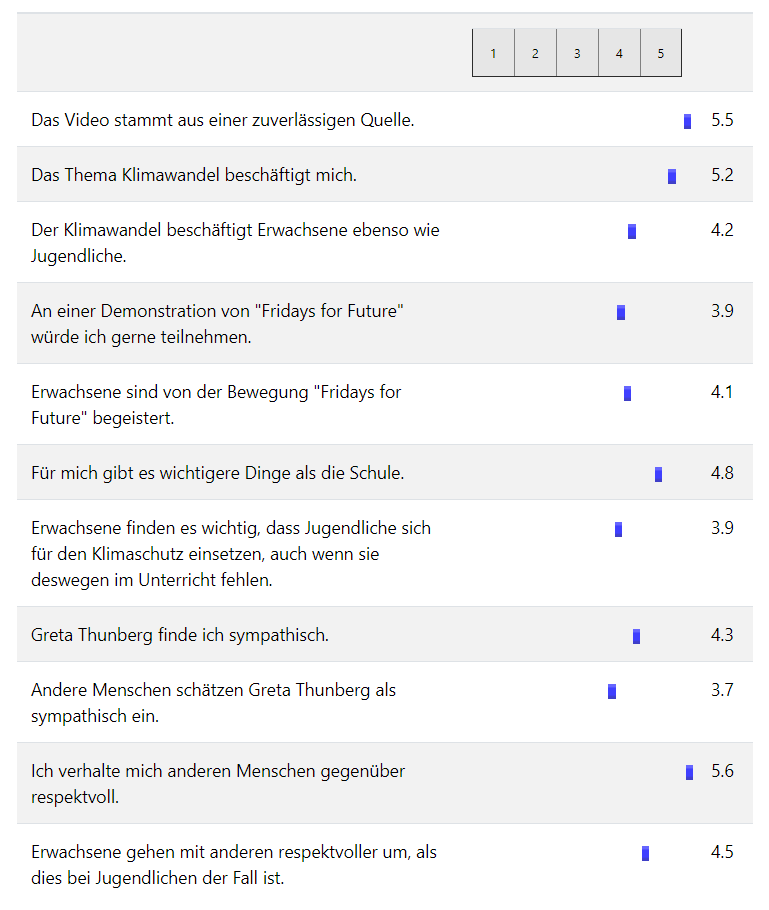
Am auffallendsten ist sicherlich, dass die Sympathie für Greta Thunberg im Vergleich zur ersten Umfrage abnahm, was darauf hindeutet, dass Hasskommentare durchaus Wirkung erzielen können. Auch die Einschätzung darüber, wie andere Greta Thunberg einschätzten, wies gegenüber der ersten Umfrage eine negativere Tendenz aus. Die Haltung der Erwachsenen gegenüber dem Klimawandel wurde ebenfalls weniger positiv eingeschätzt und die Bereitschaft an einer entsprechenden Demonstration teilzunehmen, nahm ab.

Ausserdem äussersten sich die Schülerinnen und Schüler frei darüber, was sie von den Kommentaren unter dem YouTube-Video hielten.

Ich denke viele Menschen haben das Bedürfnis, andere Leute runter zu machen. Die Sache ist nur, dass ihnen das überhaupt nichts bringt und einfach respektlos ist. Solche Kommentare sollte man lassen oder neutral schreiben.

Weshalb manche Leute beleidigende Dinge schreiben, ist für mich nicht nachvollziehbar.

Dieses Muster zog sich durch alle Kommentare, unabhängig davon, wie wichtig den einzelnen Schülerinnen und Schüler das Thema Klimawandel oder wie sympathisch ihnen die Greta Thunberg als Person ist. Auf Unverständnis stiess bei vielen auch der Aufwand, den Einzelpersonen offensichtlich betreiben, um Kommentare zu verfassen.

Zusammenfassend kann man festhalten, dass die Schüler sich motiviert mit der Thematik „Kommentare bei YouTube“ auseinandersetzten, dabei aber unterschiedliche Ansätze zum Durchforsten der Kommentare verwendeten. In Bezug auf negative Kommentare waren sich aber alle einig, dass man solche besser unterlässt. Wenn also Themen wie Hass im Internet zunehmend im Unterricht thematisiert werden, sollte man sich dabei kritisch fragen, ob damit nicht ein Problem angesprochen wird, welches die aktuelle Generation der Jugendlichen zumindest im vermuteten Ausmasse gar nicht (mehr) hat.

Weiterführende Unterlagen

Kurs der European Schoolnet Academy: Hacking Hate, https://www.europeanschoolnetacademy.eu/courses/course-v1:SELMA+Hacking_Hate+2019/about

Der grösste gemeinsame Teiler (ggT) wird in der Mathematik beispielsweise beim Gleichnamigmachen von Brüchen verwendet, er ist aber auch innermathematisch interessant. In diesem Beitrag wird anhand des ggTs gezeigt, wie die Computerunterstützung den Mathematikunterricht bereichern kann.

Zur Berechnung des ggT können verschiedene Verfahren verwendet werden.

• Teilermengen
• Primfaktorzerlegung
• Euklidischer Algorithmus

Teilermengen

Bei kleinen Zahlen ist die Verwendung von Teilermengen für die Berechnung des ggTs sinnvoll, weshalb dieses Verfahren gerne auf der Primarstufe verwendet wird. Um beispielsweise den ggT(18,24) zu berechnen, schreibt man die Teilermengen von 18 und 24 auf:

T₁₈ = {1, 2, 3, 6, 9, 18}

T₂₄ = {1, 2, 3, 4, 6, 8, 12, 24)

Es gilt also: ggT(18, 24) = 6.

Primfaktorzerlegung

Da die Menge der Teiler bei grossen Zahlen schnell übersichtlich werden kann, ist es häufig einfacher, die Zerlegung in Primfaktoren anzuwenden. Dieses Verfahren wird auf der Sekundarstufe I bevorzugt, weil Primfaktoren in der Zahlentheorie häufig auch behandelt werden. Für unser einfaches Beispiel sieht dies so aus:

18 = 2 ∙ 3 ∙ 3

24 = 2 ∙ 2 ∙ 2 ∙ 3

Die paarweise eingefärbten Primfaktoren können nun als Faktoren zur Bildung des ggTs verwendet werden: 2 ∙ 3 = 6.

Dieses Verfahren ist zwar mathematisch der Methode mit den Teilermengen vorzuziehen, aber für die Schülerinnen und Schüler weniger offensichtlich, weshalb es sich hier lohnt, eine Visualisierung zu Hilfe zu nehmen.

Das für die Visualisierung verwendete GeoGebra-Applet, ist unter diesem Link verfügbar: https://www.geogebra.org/m/dhVMBqr3. Da die einzelnen Primfaktoren der beiden gegebenen Zahlen als unterschiedlich eingefärbte Elemente (blau und rot) eines Punkteplots dargestellt werden, wird deren Schnittmenge (violett) sofort ersichtlich. Als Zusatzgewinn ist auch gleich das kleinste gemeinsame Vielfache (kgV) ersichtlich.

Auch wenn die Primfaktorzerlegung schneller zum Ziel führt als die Bestimmung der Teilermengen, kann sich doch für grosse Zahlen sehr schnell sehr aufwändig werden.

Euklidischer Algorithmus

Beim euklidischen Algorithmus werden in der einfacheren Form Differenzen, in der etwas schneller zum Ziel führenden Form Quotienten und Reste verwendet. So ergeben sich z.B. für die Zahlen 18 und 24 folgende Schritte:

Auch hier ist es für Schülerinnen und Schüler nicht einfach nachzuvollziehen, wie genau und weshalb der Algorithmus funktioniert, weshalb sich wieder ein Rückgriff auf eine Visualisierung empfiehlt. Eine solche hat z.B. die japanische Keio Universität zu Verfügung gestellt: Link zur Webseite.

Möglichkeiten der computergestützten Mathematik

Die oben gezeigten Visualisierungen laden zu weiteren mathematischen Untersuchungen ein. Im Hinblick auf den euklidischen Algorithmus ist etwa die Fragen nach Zahlenpaaren interessant, welche möglichst viele Schritte bis zur Lösung benötigen. Dazu muss natürlich der Zahlenraum eingeschränkt werden. Aber einige Versuche zeigen schnell, dass nicht unbedingt die grössten Zahlen auch die meisten Rechenschritte erfordern, und bereits im Zahlenraum 1000 ergeben sich so viele mögliche Kombinationen, dass diese nicht mehr von Hand untersucht werden können.

Deshalb lohnt es sich, den Sachverhalt mit dem Computer berechnen zu lassen. Dies kann beispielsweise mit Snap! geschehen, wobei erst einmal eine für den Computer verständliche Umsetzung des euklidischen Algorithmus geschrieben werden muss. Eine elegante Umsetzung findet sich z.B. in Donald E. Knuths „The Art of Computer Programming. Volume 1: Fundamental Algorithms“ auf Seite 2.

In Snap! kann dieser Algorithmus mit einer Rekursion umgesetzt werden:

Mit Hilfe der geschriebenen Funktion kann nun der ggT für viele Zahlenpaare berechnet werden. Färbst man zusätzlich Koordinaten (Quadrate) gemäss ihrer Iterationstiefe (Anzahl notwendige Schritte zur Berechnung), erhält man sehr schnell einen Überblick, welche Zahlenpaare interessant sind.

In der oben abgebildeten Grafik entsprechen die roten Punkte beispielsweise den Koordinaten (13, 21) und (34, 21).

Verschafft man sich einen Überblick über eine grössere Zahlenmenge, erhält man beispielsweise die Koordinaten (34, 55) und (89, 55) als interessante Werte.

Die Visualisierung hilft uns also dabei, interessante Zahlenpaare zu finden. Um die Frage nach dem Zahlenpaar mit den meisten Berechnungsschritten im Zahlenraum bis 1000 zu klären, reicht dies jedoch noch nicht aus. Hier lohnt es sich, noch einmal zur Visualisierung des ggTs durch die japanische Keio Universität zurückzukehren, wobei wir diesmal das Zahlenpaar (34, 55) verwenden:

Es lohnt sich, die Grösse der verwendeten Quadrate zu betrachten: 1, 1, 2, 3, 5, 8, 13, 21, 34, … Spätestens an dieser Stelle entdecken einige Schülerinnen und Schüler der Sekundarstufe 1 die zugrunde liegende Gesetzmässigkeit. Jede Zahl ist jeweils die Summe ihrer beiden Vorgängerzahlen, besser bekannt als Fibonacci-Folge. Indem wir diese fortsetzen, finden wir die entsprechende Lösung: … 55, 89, 144, 233, 377, 610, 987.

Die Verwendung von computergestützten Visualisierungen erleichtert es den Schülerinnen und Schüler also nicht nur, mathematische Verfahren besser zu verstehen, sie lädt auch dazu ein, selbständig oder im Dialog weitere mathematische Zusammenhänge zu entdecken. Ohne Unterstützung ist dies zwar auch möglich, eine solche Umsetzung würde aber zu viel Zeit in Anspruch nehmen und wäre weniger offensichtlich.

Das verwendete Snap!-Programm wird durch verschiedene Parameter gesteuert, diese werden im Programm selbst genauer beschrieben.

Link zum Programm: https://snap.berkeley.edu/project?user=mattgig&project=ggT

Quellen

Knuth (1997, 3rd Edition). The Art of Computer Programming. Volume 1: Fundamental Algorithms. Link: https://archive.org/details/B-001-001-249

Übung Euklidischer Algorithmus: https://www.gigers.com/matthias/schule/euklid_einfach.html

Visualisierung Euclidean Algorithm: https://gc.sfc.keio.ac.jp/fl_img/course04/ex/euclidean_animation/euclidean.html

Visualisierung ggT und kgV (GeoGebra): https://www.geogebra.org/m/dhVMBqr3

Wikipedia: Fibonacci-Folge, https://de.wikipedia.org/wiki/Fibonacci-Folge

Wikipedia: Grösster gemeinsamer Teiler, https://de.wikipedia.org/wiki/Größter_gemeinsamer_Teiler

Die Steganografie ist die Kunst, zusätzliche Informationen in einem Medium zu verstecken. In der Digitaltechnik geschieht dies häufig dadurch, dass ein bestimmtes, für Aussenstehende unauffälliges Bitmuster hinterlegt wird.

Das folgende Snap!-Beispiel verwendet eine einfachere Methode und nutzt die Tatsache, dass in einem Computersystem jeder Buchstabe auch durch eine Zahl repräsentiert werden kann. Diese Zahl wird dann einfach in einen Farbkanal von Bildpunkten geschrieben.

Programmierung in Snap!

Das Programm besteht aus zwei Teilen:

1. Im Hauptteil, welcher direkt beim Start aufgerufen wird, berechnet das Programm für jeden Buchstaben einer Geheimbotschaft den entsprechenden nummerischen Wert und verwendet diesen dann, um den Grünkanal der einzelnen Farbquadrate zu setzen. Damit diese Veränderungen im Grünkanal nicht so augenfällig sind, werden für den Blau- und den Rotkanal zusätzlich zufällige Werte gesetzt.
2. Das Auslesen der Bildinformation wird gestartet, sobald die Leertaste gedrückt wird. Dazu wird der Grünwert eines jeden Quadrates bestimmt und wieder in einen Buchstaben umgerechnet.

Um die farbigen Quadrate auf den Bildschirm zu zeichnen werden drei ineinander verschachtelte for-Schlaufen verwendet:

1. Die z-Schlaufe zeichnet die einzelnen Quadrate, deren Farbe durch jeweils einen einzelnen Buchstaben bestimmt wird.
2. Die x-Schlaufe rechnet für jeden Buchstaben den passenden Farbwert (Grünkanal) aus und zeichnet jeweils eine Zeile von Quadraten.
3. Die y-Schlaufen bestimmt, wo die Quadratzeile auf dem Bildschirm platziert wird.

Dabei benutzt das Programm zusätzliche Bibliotheken, welche erst über das Dateimenü importiert werden müssen:

Die Funktion „multiline“ aus der Bibliothek „allow multi-line text input into a block“ erleichtert die Texteingabe für die Geheimnachricht.

Verwendung der Steganografie

Bei der Verschlüsselung von Daten sorgt man heute meist für Offenheit, was bedeutet, dass die Verfahren zur Verschlüsselung offengelegt werden können und es einer Drittperson trotzdem nicht in nützlicher Frist gelingt, die Geheimbotschaft zu lesen. Bei der Steganografie hingegen versucht man die Tatsache zu verschleiern, dass überhaupt eine geheime Mitteilung besteht. Verwendung findet dieses Verfahren deshalb in folgenden Situationen:

• Bei verschiedenen Medien kann mittels der Steganografie ein Wasserzeichen eingebaut werden, welches Rückschlüsse auf die Weitergabe eines solchen Mediums zulässt. Dies ist beispielsweise dann nützlich, wenn überprüft werden soll, ob ein Copyright eingehalten wurde.
• Mittels des gleichen Verfahrens ist es aber beispielsweise auch möglich, einen Schadcode, z.B. für einen Virus, in eine dafür geeignete Computerdatei einzufügen.

Verwendung in der Schule

In der Informatik können mit dem Programmbeispiel die Konzepte Variable, verschachtelte Schlaufen und die Kodierung von Zeichen und Farben thematisiert werden. Fortgeschrittene Schülerinnen und Schüler können den Kodierungsalgorithmus so anpassen, dass das Auslesen der Informationen durch eine Drittperson erschwert wird, indem beispielsweise mehr als ein Farbkanal für die Verschlüsselung verwendet wird (Rotation oder Auswahl eines RGB-Kanals abhängig vom zuletzt verschlüsselten Buchstaben). Etwas einfacher ist die Anpassung des Farbraums durch geschicktes Auswählen der Zufallszahlen für die nicht kodierten Farbkanäle.

Natürlich können sich die Schülerinnen und Schüler auch mit Geheimbotschaften hinterlegte Bilddateien austauschen. Sie können die Bilder mit einem Rechtsklick auf die Bühnenfläche (stage) speichern.

Ebenso einfach kann ein Bild geladen werden, indem man dieses dem Hintergrund als neues Kostüm zuordnet.

Damit steht dem Austausch von geheimen Botschaften innerhalb einer Klasse nichts mehr im Wege.

Quellen

Representing Data with Images and Sound (Kurs der Rasperry Pi Foundation auf FutureLearn), https://www.futurelearn.com/courses/representing-data-with-images-and-sound

Wikipedia: Steganografie, https://de.wikipedia.org/wiki/Steganographie#Ziele_der_Steganographie

Roboter können wesentliche Prinzipien der Informatik wie die Anwendung von Sensoren und Aktoren veranschaulichen. Allerdings kann die Verwendung von Robotern auch erhebliche Kosten bei deren Anschaffung verursachen, weshalb es zumindest für die Vermittlung von Grundprinzipien sinnvoll sein kann, das Verhalten von Robotern erst einmal zu simulieren, bevor man zur Hardware greift.

Der folgende Roboter wurde in Snap! programmiert. Er verfügt über zwei einfache Sensoren, welche dafür sorgen, dass sich der Roboter in eine neue Richtung dreht. (Bei einem richtigen Roboter würden diese Sensoren die Drehzahl von Motoren steuern.) Sobald der Sensor die Farbe Schwarz meldet, dreht sich der Roboter ab.

Programmierung des Roboters

Die Programmierung des Roboters erfolgte über drei Elemente:

• Umgebung,
• Roboter und
• Sensoren.

Innerhalb der Umgebung wurde ein Zeitgeber programmiert, welcher für die Taktung der weiteren Elemente sorgt, indem jeweils ein Signal versendet wird:

Innerhalb der Umgebung wird auch die Variable für die Laufrichtung des Roboters festgelegt.

Der Roboter selbst bewegt sich in jedem Zyklus um eine bestimmte Anzahl von Schritten in die berechnete Richtung.

Der Zufallswert bei der Vorwärtsbewegung soll Abweichungen bei der Fahrt durch ein „physikalisches“ Gelände simulieren. Diese Ungenauigkeiten sorgen dafür, dass der Roboter sich nicht perfekt verhält, sondern sein Verhalten durch kleine Störungen beeinflusst werden. Lässt man hier einen grösseren Bereich zu, kann man damit Unzulänglichkeiten in der mechanischen Konstruktion nachbilden.

Ausserdem hinterlässt der Roboter eine Spur, durch welche sich sein Bewegungsmuster auch über eine längere Zeit verfolgen lässt.

Die eigentliche Steuerung des Roboters erfolgt über zwei seitlich angebrachte Sensoren:

In jeden Schritt werden die Sensoren zuerst relativ zum Roboterkörper positioniert, was bei einem richtigen Roboter nicht notwendig ist. Wenn der Sensor auslöst, wird dies durch einen Kostümwechsel (grün) angezeigt und die Richtung, in welche sich der Roboter bewegt, wird angepasst. Auch hier werden Zufallswerte verwendet, um kleine Ungenauigkeiten einzuführen.

Verwendung im Unterricht

Die Simulation dient der Veranschaulichung von grundlegenden Elementen der Robotik. Die Lernenden können in Snap! den Hintergrund gestalten, um die Grenzen der einfachen Steuerung auszuloten. Mögliche Fragestellungen sind:

• Welche Auswirkungen haben die Veränderungen von Steuerungswerten wie z.B. bei der Richtungsänderung oder Vorwärtsbewegung?
• Bei welcher Umgebungsgestaltung verhält sich der Roboter nicht so wie geplant?
• Kann die Anordnung der Sensoren für allgemeine oder spezielle Umgebungen optimiert werden?

Im Vordergrund steht hier also nicht die eigentliche Programmierung des Roboters, sondern dessen Interaktionen mit der Umgebung. Damit wird für die Lernenden schnell ersichtlich, wo die Grenzen einer einfachen Steuerung liegen und sie können damit besser nachvollziehen, weshalb die Programmierung eines komplexeren Verhaltens seine Tücken haben kann.

Quellen

Online-Kurs „Begin Robotics“ auf FutureLearn: https://www.futurelearn.com/courses/begin-robotics

Ben Ari und Mondada (2018). Elements of Robotics. SpringerOpen: https://link.springer.com/book/10.1007%2F978-3-319-62533-1

Die Raspberry Pi Foundation bietet über FutureLearn interessante Kurse zum Bereich „Medien und Informatik“ an. Einer dieser Kurse, „Representing Data with Images and Sound: Bringing Data to Life“ greift unter anderem das Thema Foto-Filter auf und bietet dazu auch einige interessante Code-Beispiele mit Python, welche die Fähigkeiten von Anfängerinnen und Anfängern wohl teilweise übersteigen. Eine Umsetzung mit Snap! erleichtert nicht nur die Programmierung, durch die Verwendung der Webcam ist auch das Einbinden von Bilddateien wesentlich einfacher.

Programmierung in Snap!

Ein geeignetes Bild kann man in Snap! mittels der Zusatzbibliothek „Pixels“ leicht über die Webcam aufnehmen.

Der abgebildete Programmcode verschiebt zusätzlich das aufgenommene Bild in die linke obere Ecke.

Ein zweites Objekt liest nun die Pixel vom Bildschirm ab, rechnet diese um und bildet das Ergebnis an einer anderen Stelle des Bildschirms ab. Der folgende Programmcode erzeugt drei Abbildungen:

• Graustufenbild: Alle drei Farbkanäle (Rot, Grün, Blau) werden auf den Wert des Rotkanals gesetzt;
• Negativbild: Für alle drei Farben wird die neue Farbe berechnet, indem der Farbwert des Kanals von 255 subtrahiert wird.
• Rotierende Farben: Jeder Farbwert wird mit einem Faktor multipliziert. Damit kein Wert grösser 255 entsteht, wird das Produkt anschliessend modulo 255 gerechnet, d.h., es handelt sich um den Rest nach einer Division durch 255.

Im Wesentlichen besteht das Programm aus zwei verschachtelten Schlaufen, die dafür sorgen, dass jeder Pixel ausgelesen wird. In der inneren Schlaufe wird der Farbwert ausgelesen, umgerechnet und ein entsprechender Pixel an der richtigen Stelle geschrieben.

Das verwendete Verfahren ist zwar sehr langsam, dafür aber recht anschaulich. Dieses kann gut anhand eines kleinen Bildes von Hand nachvollzogen werden, da die neuen Bilder zeilenweise auf dem Bildschirm erscheinen.

Verwendung im Unterricht

Foto-Filter gehören zum Alltag von Jugendlichen und werden von diesen auch gerne genutzt. Nebst dem technischen Aspekt (Medien und Informatik) kann das Beispiel auch im Kunstunterricht (Bildnerisches Gestalten) verwendet werden. Für ansprechende Farbfilter sind dabei unter Umständen schon recht komplexe Umrechnungen notwendig.

Haben die Schülerinnen und Schüler das Prinzip einmal begriffen, lädt die Aktivität zu umfangreichen Experimenten ein.

Quellen

Representing Data with Images and Sound: Bringing Data to Life: https://www.futurelearn.com/courses/representing-data-with-images-and-sound

Python: https://www.python.org

Raspberry Pi Foundation: https://www.raspberrypi.org

Snap-Programmierumgebung: https://snap.berkeley.edu/snap/snap.html

An weiterführenden Schulen ist das Zusammenfassen von Texten eine Fähigkeit, die über den Erfolg des Lernens entscheiden kann, deshalb sollte sie auf der Sekundarstufe I regelmässig geübt werden. Allerdings zeigt sich auf, dass viele Lernende damit Schwierigkeiten haben. Dabei stehen sie vor allem vor zwei Herausforderungen:

• wesentliche Schlüsselbegriffe im Text erkennen;
• sich bei der Zusammenfassung auf das Wesentliche zu konzentrieren.

Beide Schritte können mit interaktiven H5P-Übungen ohne grossen Aufwand für die Lehrperson vorbereitet werden.

Ausgangsmaterial

Gerne wird auf der Sekundarstufe I darauf verwiesen, dass Lernende sich mittels der Wikipedia selbst schlau machen könnten. Meist zeigt sich dann aber schnell: Der Schwierigkeitsgrad dieser Texte übersteigt die Lesefertigkeiten der meisten Schüler bei weitem. Als geeignetere Quelle bietet sich deshalb das Klexikon an, da dessen Texte in einer leicht verständlichen Sprache verfasst sind.

H5P-Übung

Wie auch bei der Wikipedia sind im Klexikon Schlüsselbegriffe verlinkt, was den Aufbereitungsaufwand für H5P-Übungen verringert. Nachdem der Text in eine Textverarbeitung kopiert wurde, kann er dort bearbeitet werden. H5P macht es dem Nutzer besonders leicht, weil Schlüsselbegriffe einfach markiert werden können: *Schlüsselbegriff*.

Für die Übung selbst werden zwei Aufgabentypen von H5P verwendet:

• Drag Text für den eigentlichen Lesetext,
• Fill in the Blanks für Lückentexte.

Die Schlüsselwörter aus dem Text werden also zur Rekonstruktion des Texts durch die Lernenden verwendet. Dabei üben die Schülerinnen und Schüler Voraussagen über die mögliche Fortsetzung eines Textes zu machen und die Schlüsselwörter im Text erzielen durch das Verschieben und die anschliessende farbliche Hervorhebung eine grössere Aufmerksamkeit. Damit die Lernenden bei der Erarbeitung des Textes eine unmittelbare Rückmeldung erhalten, kann man die Einstellungen für „Drag Text“ entsprechend setzen.

Für die Schülerinnen und Schüler präsentiert sich die Übung dann so (interaktives Beispiel am Schluss des Beitrags):

Nachdem die Lernenden den Text rekonstruiert haben, steht nun dessen Zusammenfassung an. Dazu wird die sogenannte „Topic – Comment“-Methode verwendet. Bei dieser Art der Zusammenfassung werden wichtige Schlüsselbegriffe durch weitere Fakten kommentiert. Dies kann relativ einfach in Form einer Liste mit Unterpunkten umgesetzt werden.

Uluru
- ein Berg in *Australien*
- ist auch unter dem Namen *Ayers* Rock bekannt

Um eine solche Liste zu schreiben, müssen die Lernenden nicht nur den Inhalt des Textes verstehen, es ist auch notwendig, dass sie sich Überlegungen zu einer sinnvollen (neuen) Struktur machen. Auf der Sekundarstufe I fällt auch dieser Schritt vielen Lernenden schwer. Eine Vorgabe durch die Lehrperson kann dabei helfen, die Schülerinnen und Schüler nach und nach an die Methode heranzuführen.

Da die Lernenden es nicht mehr mit einem neuen Lerngegenstand zu tun haben, wird nun anstelle der Zuordnungsübung ein Lückentext verwendet. Dessen Einstellungen werden wieder so gesetzt, dass Rückmeldungen unmittelbar erfolgen. Dazu aktiviert man in den Einstellungen die Option „Automatically check answers after input“.

Zusammenfassung

Das Herauslesen und Zusammenfassen von Schlüsselinformationen aus Sachtexten ist für viele Schülerinnen und Schüler der Sekundarstufe eine Herausforderung, weshalb sie schrittweise an diese Aufgabe herangeführt werden sollten. Interaktive Übungen (z.B. mit H5P) sind dabei nicht nur hilfreich, sie können von Lehrpersonen auch mit vergleichsweise kleinem Aufwand schnell hergestellt werden.

Quellen

H5P: https://h5p.org/content-types-and-applications

Klexikon: https://klexikon.zum.de

„Topic – Content“-Methode aus Online-Kurs „Improving your study techniques“: https://www.futurelearn.com/courses/improving-study-techniques

Vor Beginn eines neuen Schuljahres müssen in Moodle-Installationen diverse Wartungsarbeiten durchgeführt werden. Dazu gehört auch das Einschreiben von Schülerinnen und Schülern in den entsprechenden Lerngruppen. Diese sind wichtig, weil darüber beispielsweise die Zuordnung von Prüfungsdaten im Kalender erfolgt.

Früher war dies eine aufwändige und fehlerbehaftete Angelegenheit, denn die zu Verfügung stehenden Daten waren meist unvollständig oder mit Fehler behaftet (Namen nicht richtig geschrieben, falsche Gruppeneinteilung, Gruppennamen nicht systematisch verwendet, …). Diese Daten mussten dann ins CSV-Format umgewandelt und mit entsprechenden Anpassungen hochgeladen werden. Erfolgte bei einzelnen Schülerinnen und Schülern eine Umteilung innerhalb des Semesters, mussten die Gruppen von Hand nachgeführt werden.

Um dieses Problem auf der Sekundarstufe I zu lösen, wo sich die Gruppen spätestens auf das Semesterende durch Umstufungen wieder verändern können, kann man die Erweiterung „Gruppenwahl“ (Group Choice) einsetzen. Dabei müssen die Lerngruppen zwar immer noch definiert werden, was in der Regel nur wenige Anpassungen bedingt, die Schülerinnen und Schüler können sich nun aber selbständig in die entsprechenden Gruppen einschreiben. Dies funktioniert in der Regel sehr gut, weil die Aktivität Gruppenwahl jeweils ganz am Anfang eines Kurses platziert wird.

Damit die Lehrperson sieht, welche Schülerinnen und Schüler sich noch nicht in eine Gruppe eingeschrieben haben, ist es sinnvoll, die Option „Spalte für Teilnehmer/innen ohne Wahl“ zu aktivieren.

Falls es sich als notwendig erweist, kann die Gruppeneinteilung nach wie vor über die üblichen Werkzeuge durch die Lehrperson erfolgen oder angepasst werden. Die Lernenden können diese mit der vorgestellten Aktivität jedoch jederzeit überschreiben. Damit die Schülerinnen und Schüler ihre Wahl später anpassen können, sollte man die Option „Änderung der Wahl erlauben“ aktivieren.

Möchte man noch einen Schritt weitergehen, kann man auch Erweiterungen verwenden, bei welchem die Schülerinnen und Schüler einer Gruppe aufgrund gewisser Eigenschaften zugeteilt werden, oder bei denen sie die Gruppen selbst definieren können.

Quellen:

• Activities: Group Choice (https://moodle.org/plugins/mod_choicegroup)
  Die Erweiterung erlaubt es den Lernenden, sich in bestehende Gruppen einzuschreiben.
• Activities: Group Selection (https://moodle.org/plugins/mod_groupselect)
  Die Erweiterung erlaubt es den Lernenden, selbst Gruppen zu erzeugen und sich darin einzuschreiben.
• Activities: Group Formation (https://moodle.org/plugins/mod_groupformation)
  Lernende werden einer Gruppe aufgrund gewisser Eigenschaften zugeordnet.

Snap! eignet sich auch dafür, einfache Simulationen durchzuführen. Das vorliegende Beispiel zeigt die Simulation einer Population, deren Verhalten von den vorhandenen Ressourcen abhängt.

Die Programmierung dieser Welt wird in drei Schritten aufgebaut:

1. Die Welt schafft die Umgebung für die Lebewesen.
2. Das Futter dient als Ressource für die Lebewesen.
3. Die Lebewesen sind auf der Suche nach Futter. Der Erfolg dabei entscheidet über Tod, Weiterleben oder Vermehrung.

Die Welt

Die Welt wird durch den Bildschirm begrenzt und gibt den Zeittakt vor. Alle sechs Sekunden beginnt in der Welt ein neuer Tag. Der Tagesanbruch wird in Snap! durch eine Nachricht an alle mitgeteilt.

Sobald das Programm (grüne Flagge) gestartet wird, beginnt das Programm ein Hintergrundgeräusch (Wellen) abzuspielen. Dieser Aspekt kann auch weggelassen werden, macht die Simulation aber stimmungsvoller.

Anschliessend wird in einer Endlosschleife der Tagesablauf programmiert: Im Laufe der Zeit wird der Hintergrund immer dunkler und zu Beginn jedes Tages wird mit „broadcast“ eine Mitteilung versendet, welche sowohl die Futterquelle als auch die Lebewesen beeinflusst.

Dieser Ansatz unterscheidet sich von vielen Simulationsprogrammen, wo jeweils eine gewisse Anzahl von Schritten für jedes Objekt der Simulation berechnet wird. Die Objektorientierung von Snap! erlaubt hier die parallele Abarbeitung von Befehlen. Es wäre jedoch auch möglich, einen traditionelleren Ansatz zu verfolgen.

Das Futter

Im vorliegenden Programm verhält sich das Futter (die Ressource) passiv. Zu Beginn eines neuen Tages werden Futterstücke zufällig in der Welt verteilt. Sobald sie in Berührung mit einem Lebewesen kommen, werden sie gefressen.

Das eigentliche Programm besteht aus vier Teilen, die abhängig von Ereignissen sind:

1. Zu Beginn des Programms wird das bereits vorhandene Futterobjekt versteckt.
2. Wenn ein neuer Tag beginnt, werden alle alten Futterobjekte gelöscht und Klone des Futterobjekts erzeugt. Klone sind Objekte, welche alle Eigenschaften des ursprünglichen Objekts erben.
3. Jeder Klon wird an einer zufälligen Position auf dem Bildschirm angezeigt.
4. Wenn der Klon mit einem Lebewesen in Berührung kommt, wird er gelöscht.

Der in Snap! mögliche Ansatz des Klonens erlaubt es, die Programmierung sehr einfach zu halten. Ausserdem kann das Verhalten der Klone an zentraler Stelle sehr einfach angepasst werden. So wären nur wenige Befehle im Block „When I start as a clone“ notwendig, um die Futterteilchen in der Welt herumschwimmen zu lassen.

Die bereits vorhandene Variable „lifespan“ könnte dazu genutzt werden, dass die Futterteilchen mehr als einen Tag zu Verfügung stehen.

Die Lebewesen

Die Lebewesen irren zufällig in der Welt herum (random walk). Wenn sie auf den Bildschirmrand treffen, drehen sie sich um und setzen ihre Bewegung fort.

Auch die Programmierung der Lebewesen gliedert sich in vier Teile, welche abhängig von Ereignissen sind:

1. Bei Programmstart wird das eigentliche Objekt versteckt und Klone werden erzeugt.
2. Jeder Klon wird initialisiert, begibt sich an eine zufällige Stelle auf dem Bildschirm und wandert zufällig herum. Die Anzahl der bereits gefressenen Futterteilchen wird laufend angezeigt. Entfernt man den Befehl „say(food)“ fällt diese Anzeige weg.
3. Wenn ein Lebewesen auf ein Futterteilchen stösst, wird die Variable „food“ erhöht.
4. Zu Tagesbeginn sterben alle Lebewesen aus, welche über keine Futterreserven mehr verfügen. Wenn sie genügend gefressen haben, vermehren sie sich.

Vorteile von Snap! bei Simulationen

Durch die objektorientierte Programmierung, die Möglichkeit Nachrichten zu verschicken und die vorhandenen Befehle (z.B. zu Kollisionen) fällt das Schreiben einfacher Simulationen in Snap! leicht. Hat man einmal verstanden, wie eine solche einfache Simulation funktioniert, kann man diese durch zusätzliche Objekte komplexer gestalten oder zu einem interaktiven Spiel ausbauen.

Dabei kann es sich lohnen, die Simulation erst einmal mit Hilfe von realen Objekten durchzuspielen (z.B. mit Legosteinen), damit man eine bessere Vorstellung davon erhält, welche Ereignisse notwendig sind, damit die Programmierung funktioniert. Beim Ausprobieren der Simulation lohnt es sich auf jeden Fall, mit kleinen Anzahlen von Objekten zu beginnen. Dies vereinfacht es nicht nur, den Überblick zu behalten, sondern funktioniert auf leistungsschwachen Geräten auch reibungsloser.

Verwendung im Unterricht

Simulationen können im Unterricht breit eingesetzt werden. Während das vorliegende Beispiel sich vor allem für die Biologie eignet, kann die Simulation von Teilchen wichtige Konzepte der Physik veranschaulichen. Baut man die Simulation zu einem interaktiven Spiel aus, wird zusätzlich das Erzählen von Geschichten wichtig (Deutsch). Die Gestaltung der Futterquellen und der Lebewesen kann sehr einfach erfolgen, je nach Interesse der Schülerinnen und Schüler kann diese auch bis hin zu animierten Objekten ausgebaut werden (Bildnerisches Gestalten).

Snap! 5.0 verfügt über mächtige Befehle zum Darstellen von Landkarten.

Wenn man die Befehle für die Kartendarstellung dem Hintergrund zuordnet, kann man anschliessend beliebige Objekte auf der Karte platzieren. Dazu sind nur gerade drei Befehle notwendig:

Damit der Kartenausschnitt beliebig verschoben und gezoomt werden kann, wurde eine Steuerung über die Pfeiltasten und die Plus- und Minustaste implementiert. Der Broadcast-Befehl sorgt dafür, dass beim Verschieben und Zoomen der Karte die eingezeichneten zusätzlichen Objekte am richtigen Ort positioniert werden.

Diese Objekte können von Hand eingetragen werden, besser ist es aber sicher, wenn man mit einer Liste (mit Längen- und Breitengraden) arbeitet.

Unter Umständen bereitet die Bereitstellung der Liste Schwierigkeiten, weil die meisten Geolocation-Dienste unterdessen nur noch nach einer Registrierung oder gegen Bezahlung nutzbar sind. Für die Schweiz allerdings bietet das Geoportal des Bundes eine schulfreundliche Lösung: Adressen können in eine Exceltabelle eingetragen werden und diese generiert dann automatisch die entsprechenden von Snap! lesbaren Koordinaten.

Verwendung in der Schule

Mit den vorgestellten Befehlen von Snap! können Schülerinnen und Schüler auf einfache Weise ein rudimentäres Geografie-Informations-System aufbauen. Diese können für die verschiedensten Zwecke eingesetzt werden: Von Standort der Klassenmitglieder über die grössten Städte der Welt bis hin zur Darstellung aktiver Vulkane auf der Weltkarte. Je nach Interessen der Lernenden können unterschiedliche Objekte visualisiert werden. Verwendet man zusätzlich mehrere Kostüme, kann die Darstellung auch mit unterschiedlichen Symbolen erfolgen.

Hinweis: Die Schülerinnen und Schüler sind es gewohnt, dass sie den Standort ihrer Kolleginnen und Kollegen über die Dienste sozialer Netzwerke jederzeit anzeigen lassen können. Die Möglichkeiten von Snap! geben ihnen einen Einblick, wie solche Dienste funktionieren.

Quellen

Einfach Koordinaten von Adressen in der Schweiz generieren (Geoportal des Bundes)

Telefonbuch zum Finden von Adressen: https://tel.search.ch oder https://tel.local.ch/de

Ein Höhenmodell für die Schweiz kann man in Snap! mit wenigen Zeilen schreiben. Dazu wandelt man erst einmal die Daten des Höhenmodells (Quelle siehe weiter unten) in eine CSV-Datei um, indem man in der Originaldatei die Leerschläge durch Strichpunkte ersetzt. Anschliessend kann man die Datei einfach auf die Programmieroberfläche ziehen. Snap! wandelt die Datei automatisch in eine Variable (oder besser eine Liste von Listen) um.

Auf einzelne Elemente einer Liste kann man einfach mit folgendem Befehl zugreifen:

Da die Koordinaten der Schweizer Landeskarte von für die x-Werte von ca. 500’000 – 800’000 und für die y-Werte von ca. 70’000 – 300’000 reichen, müssen diese zuerst in die Bildschirmkoordinaten von Snap! umgerechnet werden.

Dafür eignet sich eine entsprechende Funktion:

Nun müssen an den einzelnen Bildschirmkoordinaten nur noch Punkte mit einer der Höhenangabe entsprechenden Farbe gezeichnet werden.

Das ganz Programm kann dann etwa so aussehen:

Wie bei grossen Datenmengen üblich lohnt es sich, in der Versuchsphase mit einem reduzierten Datensatz zu arbeiten. Damit können Fehler schnell korrigiert werden, ohne dass man jedes Mal lange warten muss. Im Programm funktioniert dies so, dass z.B. nur für jeden zwanzigsten Punkt Daten ausgelesen und gezeichnet werden.

Verwendung im Unterricht

Das Höhenmodell bietet eine gute Gelegenheit mit einem einfachen Beispiel in das Thema „Big Data“ einzusteigen. Im vorliegenden Fall ist der Datensatz gross, weil er sehr viele Werten enthält. Die Datenstruktur hingegen ist einfach.

Bei der Visualisierung kann man sich zusätzlich überlegen, welche Farbmodelle zum Einsatz kommen sollen, um die Höhenunterschiede von rund 5000 m in der Schweiz grafisch darzustellen.

Im Geografieunterricht kann das Modell zusätzlich verwendet werden, um verschiedene Höhenstufen darzustellen. Im einfachsten Fall färbt man einfach alle Höhenwerte blau ein, die grösser als ein kritischer Wert sind, und bekommt so ein Modell, welches einen ansteigenden Meeresspiegel visualisiert. Den gleichen Trick kann man für hohe Werte anwenden, um beispielsweise durch Weissfärbung eine mögliche Gletscherbedeckung zu simulieren. Dies dürfte dann unweigerlich zur Frage führen, wie es denn in anderen Gebieten der Welt aussieht. Vorausgesetzt man findet die passenden Daten, kann man das Programm entsprechend anpassen. Allerdings muss man dann sehr wahrscheinlich noch die entsprechenden Koordinaten umrechnen.

Quellen:

Das digitale Höhenmodell der Schweiz mit einer Maschenweite von 200 m

Schweizer Landeskarte