Das Rechnen mit Brüchen ist für viele Schülerinnen und Schüler eine Herausforderung, weil gleichzeitig neue Konzepte vermittelt werden, welche der Intuition der Lernenden teilweise widersprechen, und der automatisierte Umgang mit verschiedenen Rechengrundoperationen zentral ist. (Schwierigkeiten mit den Grundoperationen können zu einer Überlastung des Arbeitsgedächtnisses führen, welche ein erfolgreiches Erlernen zentraler Strategien im Umgang mit Brüchen behindert.) Da die Sicherheit im Umgang mit Grundoperationen vor allem in der Primarschule erworben werden muss, soll sie hier nicht weiter thematisiert werden. Dieser Beitrag konzentriert sich vielmehr darauf, wie Konzepte durch Visualisierungen mit GeoGebra helfen können, diese selbst dann zu verstehen, wenn das eigentliche Rechnen sich als schwierig erweist.
Die Visualisierungen werden gemäss dem Aufbau des Bruchrechnens in vielen Lehrmitteln vorgestellt:
- Vorstellung von Brüchen
- Addition und Subtraktion
- Multiplikation und Division
Vorstellung von Brüchen
Traditionell wird die Vorstellung von Brüchen gerne anhand von Flächen (z.B. in der Form von Tortenstücken) vermittelt. Diese Vorgehensweise hat sich bewährt, sollte aber durch die Vorstellung des Bruchs als Zahl und als Verhältnis ergänzt werden, da sonst die Lernenden eine einseitige Vorstellung davon entwickeln können, was ein Bruch ist.
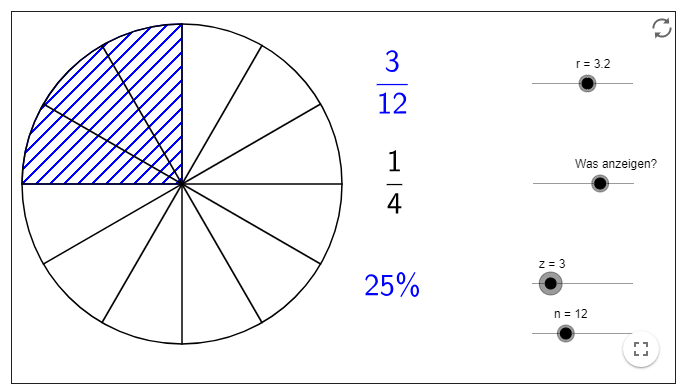
Applet: https://www.geogebra.org/m/TYfyJDqD
Bei der Visualisierung von Brüchen als Torten sollte unbedingt gezeigt werden, dass der Bruch nicht von der Grösse der Torte abhängig ist. Im vorliegenden Applet kann dazu der Radius der Torte angepasst werden. Vielmehr muss immer wieder betont werden, dass ein Bruch das Verhältnis von zwei Zahlen (Zähler und Nenner) abbildet.
Aus diesem Grund ist eine Kombination der Visualisierungen „Bruchtorte“ und Zahlenstrahl hilfreich:
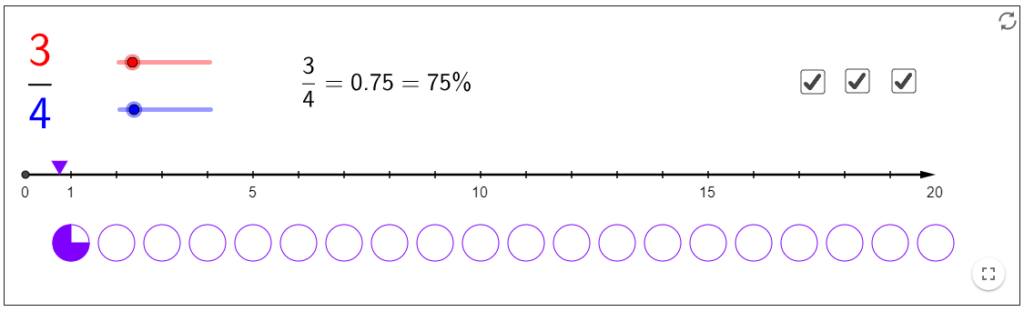
Applet: https://www.geogebra.org/m/Ecyc8FVX
Da bei diesem Applet einzelne Darstellungsformen (Bruch als Torte, Position auf dem Zahlenstrahl, Bruch, Dezimalzahl oder Prozentzahl) ausgeblendet werden können, eignet es sich gut dafür, die Lernenden Vermutungen zu den einzelnen Darstellungsformen äussern zu lassen und diese dann im gemeinsamen Gespräch zu konkretisieren. Bei entsprechenden Vorwissen der Lehrperson über typische Fehlvorstellungen von Schülerinnen und Schülern, können solche bewusst thematisiert werden. Allerdings ist dabei zu bedenken, dass eine einmalige Thematisierung meist nicht ausreicht, fehlende Vorstellungen oder Fehlvorstellungen nachhaltig zu entwickeln, respektive zu korrigieren.
Haben die Schülerinnen und Schüler einmal eine Vorstellung von der Grösse einzelner Brüche entwickelt, kann ihre Erfahrung durch das Vergleichen von Brüchen auf dem Zahlenstrahl gezielt erweitert werden, ohne dass bereits auf die formellen Methoden Kürzen und Erweitern zurückgegriffen werden muss.
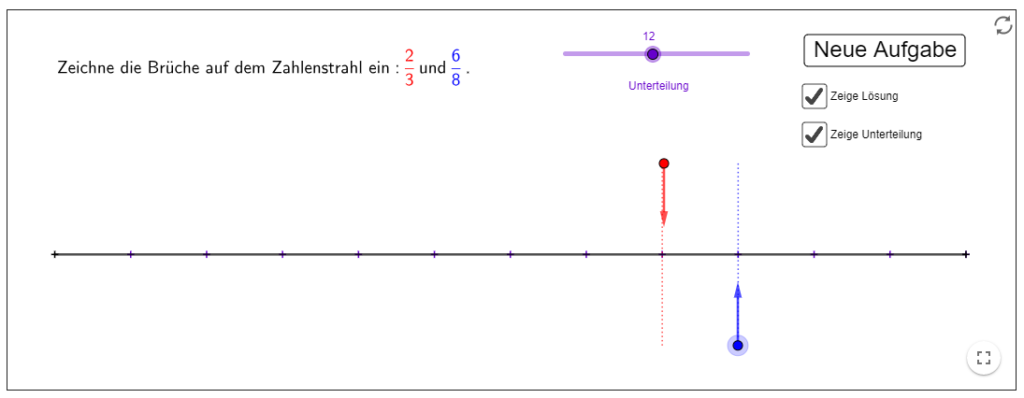
Applet: https://www.geogebra.org/m/kDKUKZk7
Auch hier ist es wieder möglich, einzelne Elemente auszublenden. Als hilfreich erweist sich bei der Diskussion mit den Schülerinnen und Schülern vor allem die Möglichkeit, den Zahlenstrahl (hier von 0 bis 1) entsprechend zu unterteilen.
Je nach Aufgabenstellung fällt die Positionierung und die Unterscheidung der beiden Brüche mehr oder weniger leicht. Eng beieinander liegende Brüche führen zur Erkenntnis, dass eine blosse Schätzung möglicherweise nicht mehr ausreicht und deshalb formellere Methoden zur Vergleichbarkeit von Brüchen benötigt werden.
Bevor darauf näher eingegangen wird, soll aber auch noch die Darstellung von Brüchen als Verhältnis (Proportion) erwähnt werden. Oftmals ist es den Lernenden überhaupt nicht bewusst, dass Brüche, Prozentzahlen und Proportionen auf dem Konzept der rationalen Zahlen aufbauen und insbesondere die Proportion sich auch im Steigungsbegriff direkt wiederfindet.

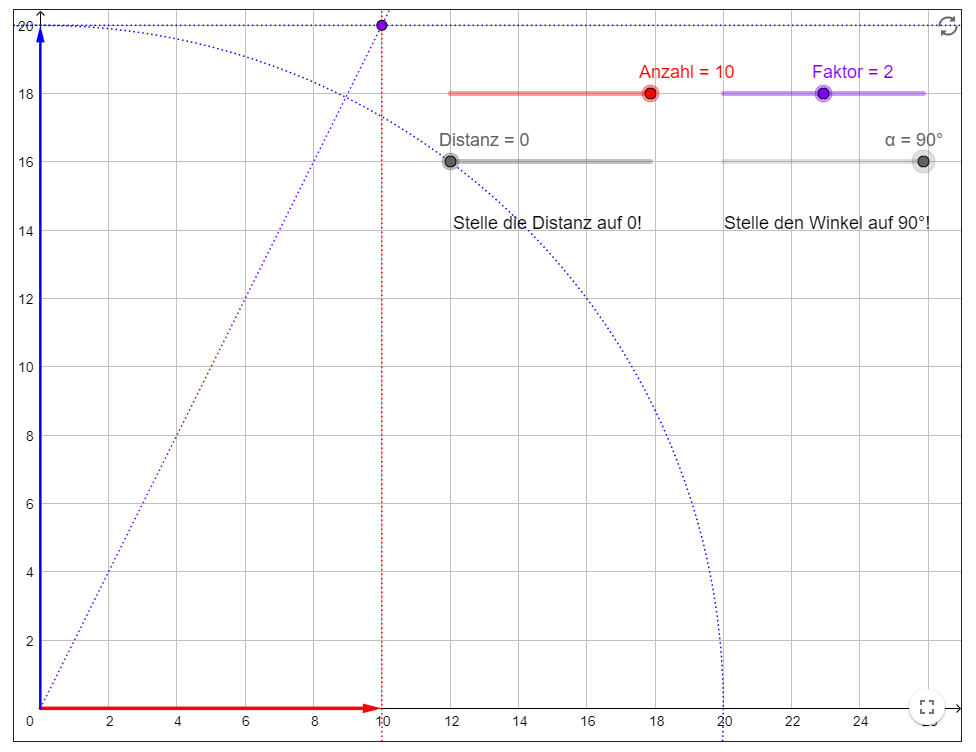
Applet: https://www.geogebra.org/m/NVeyPfYy
Durch die grafische Darstellung und das Verschieben und Drehen der einzelnen Elemente wird der Zusammenhang zwischen Verhältnis (Bruch) und Steigung (mit Steigungsdreieck) unmittelbar ersichtlich. Die Visualisierung muss nicht zwingend im Thema „Bruchrechnen“ eingesetzt werden, kann aber später (insbesondere bei der Steigung) zum Anknüpfen an vorhandenes Vorwissen eingesetzt werden.
Auch der Zusammenhang zwischen Brüchen und dem Prozentbegriff ist vielen Schülerinnen und Schülern nicht unmittelbar klar. Hier kann es helfen, wen zwei Strecken miteinander verglichen werden und die eine als Bruchteil der anderen dargestellt wird. In Kombination mit einem virtuellen Prozentgummiband kann nun der Vergleich zwischen Bruch und entsprechendem Prozentwert visuell erfasst werden.
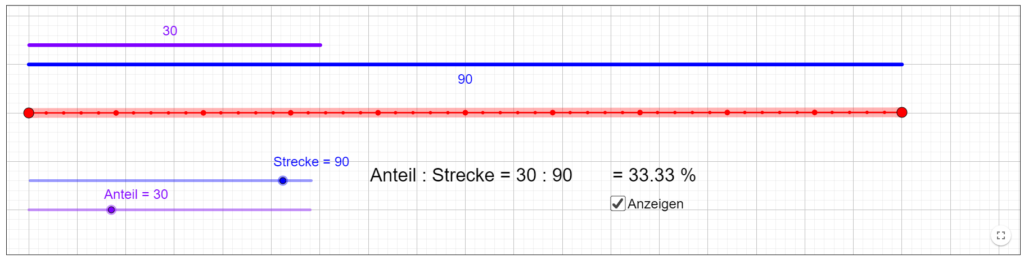
Applet: https://www.geogebra.org/m/NVeyPfYy
Diese Aktivität kann unter entsprechenden Anleitung auch dazu genutzt werden, den Vergleich von Brüchen durch Kürzen und Erweitern vorzubereiten, indem man beispielsweise die Lernenden nach weiteren Streckenpaaren suchen lässt, welche einen bestimmten Prozentwert aufweisen. Auch hier gilt selbstverständlich: Die Visualisierung sollte immer nur so lange als nötig eingesetzt werden, da das Ziel die Entwicklung des Zahlbegriffs von Brüchen ist. Da bei vielen Lernenden eine solche Vorstellung erst teilweise ausgeprägt ist, lohnt es sich auch hier, zu gezielten Experimenten anzuregen. Mit zunehmenden Masse dient die Visualisierung dann nur noch der Überprüfung der immer sicheren Vermutungen der Schülerinnen und Schüler.
Additon und Subtraktion von Brüchen
Haben die Schülerinnen und Schüler eine Vorstellung von Brüchen entwickelt, können diese in einem nächsten Schritt addiert und später auch subtrahiert werden. Dabei ist unbedingt darauf zu achten, dass die Lernenden sich darüber im Klaren sind: Die zu addierenden oder subtrahierenden Bruchstücke müssen immer gleich gross ein. Deshalb ist die Erarbeitung des Erweiterns und Kürzens von Brüchen eine Grundlage für Anwendung der Strichoperationen.
Das Erweitern und Kürzen von Brüchen mit dem Ziel, diese gleichnamig zu machen, kann relativ einfach visualisiert werden, indem Einheitsquadrate entweder längs oder quer (zusätzlich) unterteilt werden:
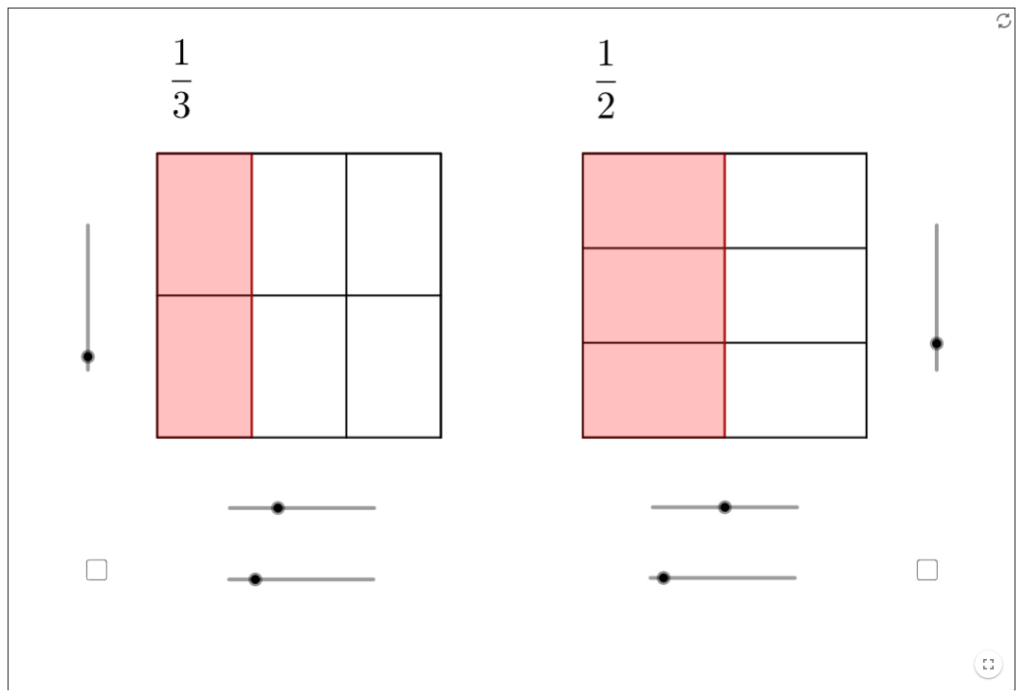
Applet: https://www.geogebra.org/m/Yf2XcAdt
Den Schülerinnen und Schülern ist möglicherweise nicht klar, dass eine der rot eingefärbten Flächen im linken Quadrat gleich gross sein muss wie eine der entsprechend eingefärbten Flächen im rechten Quadrat. Deshalb lohnt es sich, diesen Umstand sorgfältig herauszuarbeiten.
Die eigentliche Visualisierung der Addition von Brüchen kann dann wieder gut mithilfe der Tortendarstellung durchgeführt werden.
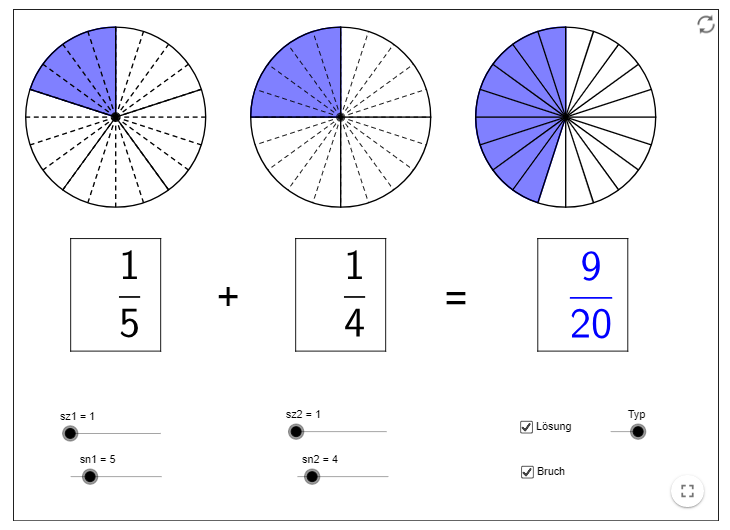
Applet: https://www.geogebra.org/m/MMBKzeeM
Haben die Schülerinnen und Schüler das Konzept der Addition verstanden, ist das Einschalten einer entsprechenden Übungsphase zwingend notwendig. Dabei kann es sich als hilfreich erweisen, wenn die ersten Rechenschritte durch weitere Visualisierungen unterstützt werden. Das Tempo der Ablösung von dem „Hantieren“ mit Tortenstücken hin zur rein formalen Berechnung mit gleichnamig gemachten Brüchen (Hauptnenner finden und Zähler umrechnen) kann sehr individuell ausfallen. Sobald die Lernenden die entsprechende Sicherheit gewonnen haben, kann die Subtraktion in der Regel ohne weitere Visualisierungen problemlos eingeführt werden.
Die einzige Schwierigkeit bei der Subtraktion stellt sich im Zusammenhang mit der Darstellung von negativen Brüchen. Den wenigsten Lernenden ist klar, dass die folgenden Darstellung gleichwertig sind: \(-\frac{a}{b}=\frac{-a}{b}=\frac{a}{-b}=-\frac{-a}{-b}\).
Eine weitere Möglichkeit, die Addition und Subtraktion von Brüchen einzuüben bietet die Bruch-Uhr:
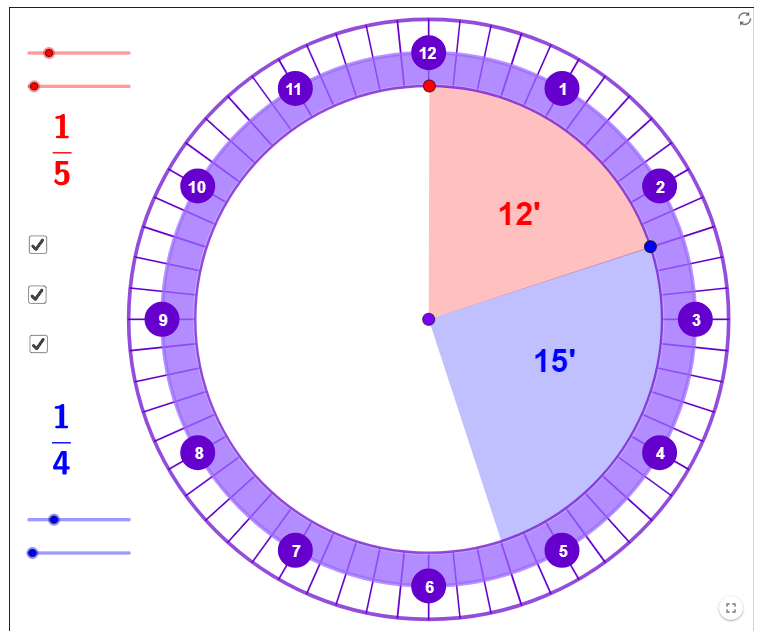
Applet: https://www.geogebra.org/m/fFeBVgYC
Mit der Umrechnung in Stunden und Minuten können an der Bruch-Uhr Zweitel, Drittel, Viertel … nachvollziehbar dargestellt werden. Gleichzeitig bietet die Bruch-Uhr eine Gelegenheit, zum Berechnen von Bruchteilen von Massen überzuleiten.
Multiplikation und Division
Die Rechenregeln zur Multiplikation von Brüchen sind einfach und die Schülerinnen und Schüler können diese mithilfe des folgenden Applets meist selbst herleiten:
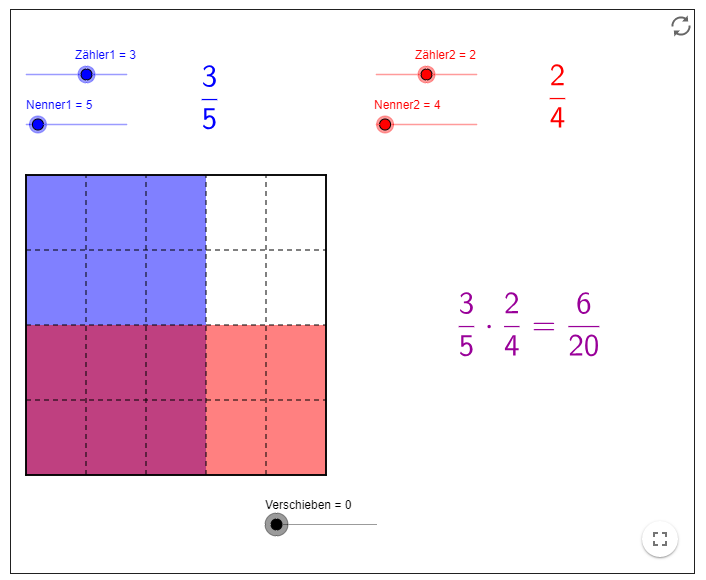
Applet: https://www.geogebra.org/m/JKCeDruf
Das Verschieben des einen Einheitsquadrates über das andere veranschaulicht die Multiplikation von Brüchen. Da gleichzeitig die entsprechende Rechenoperation sichtbar ist, gelingt es den meisten Schülerinnen und Schülern schon nach zwei bis drei Beispielen, die entsprechenden Regeln selbst zu formulieren.
Ein für einige Lernende erstaunlicher Umstand ist, dass das Resultat einer Multiplikation mit einem Bruch kleiner ist als die ursprüngliche Zahl. Es lohnt sich diesen Umstand zu thematisieren, da die Schüler in der Primarschule die Erfahrung gemacht haben, dass eine Multiplikation immer zu einem „Mehrwert“ führt.
Möchte man auch Multiplikationen über das Einheitsquadrat hinaus darstellen, muss die Zeichenfläche entsprechend erweitert werden. Im folgenden Beispiel werden die beiden Brüche als rechtwinklig zueinanderstehende Pfeile, das Resultat wieder als Fläche dargestellt:
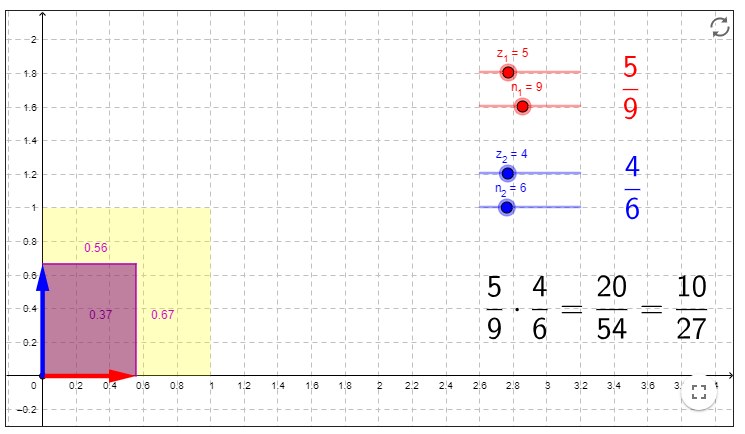
Applet: https://www.geogebra.org/m/ueZRxJNd
Nun ist es auch möglich, Multiplikationen wie \(\)2\cdot\frac{1}{3}[\latex] darzustellen. Die gleichzeitige Sichtbarkeit der Rechnung hilft auch hier, den Zusammenhang zwischen Darstellung und eigentlicher Rechnung zu verdeutlichen.
Während die Multiplikation sehr schnell verstanden wird, sieht dies bei der Division anders aus. „Brüche dividiert man, indem man den ersten Bruch mit dem Kehrwert des zweiten multipliziert“, dieser Merksatz beschreibt zwar das technische Vorgehen, dieses ist für viele Schülerinnen und Schüler aber wenig einsichtig. Dementsprechend häufig sind auch Fehlmanipulationen beim Dividieren von Brüchen. Auch hier kann es sich deshalb lohnen, entsprechende Visualisierungen zu verwenden. Hierzu kann man auf die Darstellung von Brüchen auf den Zahlenstrahl zurückgreifen und sich überlegen, wie viele Male der eine Bruch im anderen Platz findet.
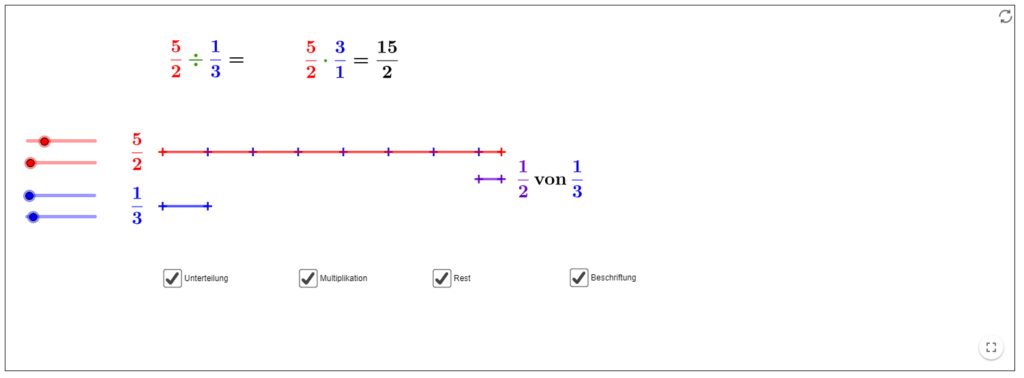
Applet: https://www.geogebra.org/m/yF9TGPh7
Das Beispiel visualisiert, wie oft der kleinere Bruch im grösseren Platz findet. Abhängig vom mathematischen Abstraktionsvermögen der Schülerinnen und Schüler kann man diesen Vergleich vorgängig auch mithilfe von verschieden langen Papierstreifen durchführen. Wie bei der Visualisierung ist dabei wesentlich, dass die Lernenden auf das bereits bekannte Verfahren des Längenvergleichs zurückgreifen können, dass sie beispielsweise vom Doppelmeter her kennen. Unter Umständen lohnt es sich auch, mit Aufgabenstellungen zu beginnen, welche aufgehen und erst danach Aufgaben zu thematisieren, bei denen ein Rest in Form eines Bruches übrigbleibt.
Fazit
Die Verwendung von Visualisierungen kann dabei helfen, Schülerinnen und Schüler eine Einsicht in den mathematischen Umgang mit Brüchen zu erlauben. Meist werden für entsprechende Demonstrationen oder angeleitete Versuche nur wenige Minuten gebraucht. Da dabei Fehlvorstellungen korrigiert und Regeln teilweise selbständig erworben werden, wird eine solche Investition durch eine Verringerung der Fehlerzahl beim anschliessenden arithmetischen Umgang mit Brüchen mehr als kompensiert. GeoGebra bietet dazu Hand, die Visualisierungen technisch umzusetzen, indem die Lehrperson diese selbst erstellt oder einfach auf einen bereits vorhandenen grossen Fundus zugreift.
Weiterführende Hinweise
Friday Institute: Fraction Foundations – Helping Students Understand Fractions
Die Teilnahme an diesem Kurs in englischer Sprache führte nicht nur zu vielen interessanten Diskussionen, sondern hat auch zur Erweiterung der eigenen Sammlung an Applets für das Bruchrechnen beigetragen.
GeoGebra: Applets zum Bruchrechnen
GeoGebra bietete eine Vielzahl von Applets zum Thema Bruchrechnen, die zur Demonstration im angeleiteten Unterricht oder bei der individuellen Arbeit verwendet werden können.
IES Practice Guide (2010). Developing Effective Fractions Instruction for Kindergarten Through 8th Grade: National Center for Education Evaluation and Regional Assistance, PDF [abgerufen 2.9.2018]
